Consider a circular ring of radius R as shown in Figure 11.21. Let the mass per unit length of the ring is m. To find the mass moment of inertia of the ring about the diametral axis XX, consider an element of length ds = rdθ; the distance of the element from the diametral axis XX is R sin θ; and mass of the element is mrdθ.
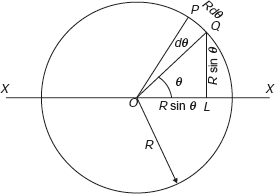
Figure 11.21 Mass Moment of Inertia of a Circular Ring
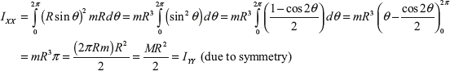
The moment of inertia about an axis passing through the centre of the circle and perpendicular to the plane of circular ring
IZZ = IXX + IYY = MR2
Leave a Reply