Mass Moment of Inertia of a Circular Disc

Consider an element of the disc of arc length rdθ, width dr, and thickness t. ρ is the mass density of the disc. Mass moment of inertia of the disc can be calculated as shown in Figure 11.22.

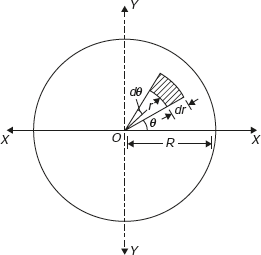
Figure 11.22 Mass Moment of Inertia of a Circular Disc

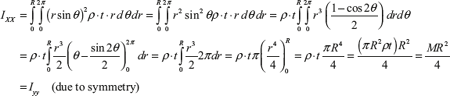
Moment of inertia perpendicular to the plane of the circular disc