All of the experimental demonstrations above have looked at the particle nature of light using billions of photons. Wouldn’t it be more convincing if we could observe a single particle of light at a time?
The setup of Figure 33 gives us an opportunity to detect individual photons. The detector is the PMT probe that we just built, and single photons are produced by dimming a laser through very dark photographic filters down to the level where only a few photons reach the photocathode every second.67
Figure 33 In this setup to detect single photons, (a) a laser beam is dimmed by very dark filters so that only a single photon reaches the PMT at any given time. (b) We used a heliumneon (HeNe) laser, but you can use any laser pointer by making the right adjustments to the system to match your laser’s power and wavelength, including accounting for the PMT’s quantum efficiency. (c) Our setup showing the high-voltage power supply (Figure 31) to bias the PMT, PMT probe (Figure 30) with the optical tube installed, the amplifier/discriminator (Figure 34), and the HeNe laser.
Figure 34 The PMT signal-processing circuit amplifies the narrow pulses detected by the PMT. The discriminator stage removes small pulses produced by thermal noise in the tube. A pulse stretcher outputs pulses that can be heard on a speaker.
Let’s work out the level of attenuation needed so that only one photon reaches the PMT in one second. We use a HeNe laser in our setup, which puts out photons at a wavelength λ = 632 nm. According to Einstein’s proposition, each photon from our HeNe laser has an energy of:
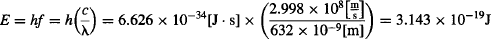
where c is the speed of light and λ is the wavelength of light (in this case 632 nm).
Our HeNe laser produces 5 mW of power, so we can calculate how many photons are emitted by the laser each second:
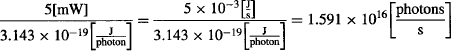
This means that we need to use very dark filters to drastically cut down on the number of photons that make it to the PMT. If we want only one photon per second to reach the PMT, we need to let only one photon out of 1.591 × 1016 photons through the filter. You could go to the beach on Venus with sunglasses that dark!
A dark photographic filter is called an attenuator, and the best kind for our purpose is a “smoked-glass” type known as a neutral-density filter. These attenuators weaken the beam with no significant dependence on wavelength. The darkness of a neutral-density filter is called optical density (D), which is defined as the base-10 logarithm of the desired attenuation.
Ideally, to have a single photon reach the PMT we need to attenuate the beam using a neutral-density filter with an optical density D = log10(1.591 × 1016) = 16.20. However, as Figure 33b shows, the RCA 6655A PMT will respond to only 1% of 632 nm photons impacting on its photocathode. In addition to the neutral-density filters, we added two narrow band-pass filters tuned to our laser’s wavelength, so that stray photons in the room cannot reach the PMT tube.|| Each of these filters allows only 45% of the desirable 632 nm photons through. We can thus recalculate the density needed to cause 1 photon/s to be absorbed by the photocathode in our setup:
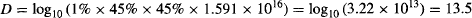
There are other real-world effects that cause photon losses, so a good start is to use D = 10 and then work your way up to yield about one laser photon detection per second.
We purchased our neutral-density filters from Thorlabs and the laser-line filters from Edmund Optics (model 43133). We opted to standardize our optical component mounting on Thorlabs’ series of SM lens tubes, so we bought our filters premounted inside SM1L03 cells. By the way, the total density of a stack of filters is simply the sum of their individual densities, so to get D = 13, we used two D = 5 and three D = 1 neutral-density filters.
Since the peak response of the RCA 6655A photomultiplier is close to 400 nm, you can get better quantum detection efficiencies if you have a green (λ = 532 nm) or violet (λ = 405 nm) laser pointer available. You will also need to change the filters to ones compatible with your laser’s wavelength. Finally, you will need to recalculate the overall number of photons after the neutral-density filters, since the number of photons emitted at a set power depends on their wavelength. For example, a 5-mW green laser will produce “only” 1.34 × 1016 photons/s, or almost 16% fewer photons than a HeNe laser of the same power.
Figure 34 shows the circuit needed to turn the PMT detections into audible clicks. Despite the enormous gain of the PMT, the signals produced by our photomultiplier probe are very small when illuminated by just a few photons at a time. A preamplifier is thus needed to easily interface the probe with other instrumentation. Our PMT probe outputs a very fast,** negative-going pulse every time that a photoelectron is produced at the photocathode. Op-amp U1 is configured as an inverting charge-sensitive amplifier, which is one of the most common ways of detecting signals from a PMT’s anode.
The positive-going pulses coming from the charge-sensitive preamplifier are turned into a Gaussian pulse by first differentiating (high-pass filtering) and then integrating (low-pass filtering) them using the circuits built around U2A and U2B. Trimmer R23 is used for pole cancellation to yield as clean a Gaussian pulse as possible through this simple configuration.
Pulses are amplified by U2C. The gain of this stage is selected via SW1. U3 is a comparator, which is used to convert pulses over a preset threshold into inverse-logic digital pulses that indicate a photon strike. This stage gets rid of small-amplitude pulses caused by thermal noise in the PMT, and is commonly known as a discriminator in physics instrumentation. Lastly, the pulses are stretched by one-shot U4 to provide an audible “click” through the piezo speaker. We added a buffer amplifier U2D so that the amplifier’s analog signal may be observed on an oscilloscope. In addition, we provided an output from the discriminator to trigger other data acquisition equipment. We will use these outputs in a later experiment.
When in operation, this setup produces an irregular series of random clicks. Fine-tune the discriminator threshold so the clicking disappears when the laser is off. Increasing the photon count to around 10 photons/s (by reducing the attenuation) makes for a signal that is much easier to detect. The output should sound like the clicking of a Geiger counter, and you may need to assure others within earshot that you are not playing with radioactive materials (yet).
Counting clicks while playing with attenuation should convince you that each count is indeed the result of a single photon being detected by the apparatus, demonstrating the existence of Einstein’s quanta as individual particle entities.††
Leave a Reply