Linear functions

A linear affine function has the following general form:

Figure 2.7 shows a few linear functions. Strictly speaking, only the first function is linear. A function f is linear if the following condition holds:

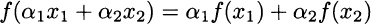
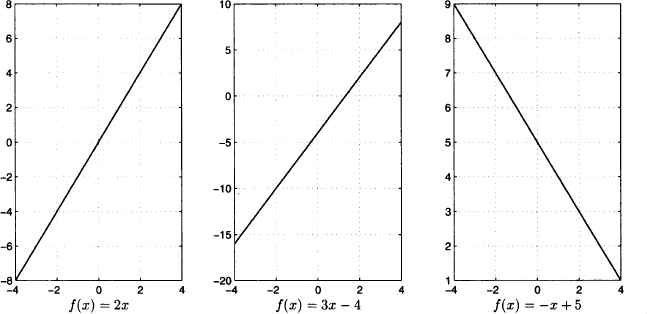
Fig. 2.7 Graphs of linear (affine) functions.

for arbitrary numbers α_i and x_i, i = 1, 2. However, this holds only when the coefficient q in (2.4) is zero. To see this, note that, for a generic linear affine function,

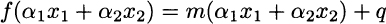
whereas

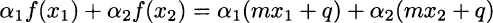
Equating the two expressions leads to q = 0. Nevertheless, we will often use the term “linear” in a loose sense, referring to linear affine functions. Since coefficient q is the value of f when x = 0, it represents the value of coordinate y at which the graph crosses the vertical axis. In fact, coefficient q is called the intercept, whereas coefficient m represents the slope of the linear function. The concept of slope is linked to the increment ratio of a function.

DEFINITION 2.3 (Increment ratio) Given a function f and two points x_a and x_b, such that x_a < x_b, the increment ratio of f over those two points is defined as

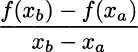
The increment ratio is the average rate at which the function increases (or decreases, if the ratio is negative) over the interval [x_a, x_b].

For a linear function, the increment ratio is

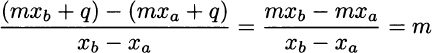
This is always the same for any pair of point; indeed a linear function is characterized by the fact that its slope is constant and tells us by how much the function changes for a unit change in the independent variable (the reader is invited to check the slopes of linear functions in Fig. 2.7). We may specify a particular line by giving its slope m and its intercept q, i.e., the vertical coordinate of the point (0, q) at which it crosses the vertical axis. Alternatively, we can specify a line by giving its slope and one point (x₀, y₀) through which the function passes. This line is represented by the equation

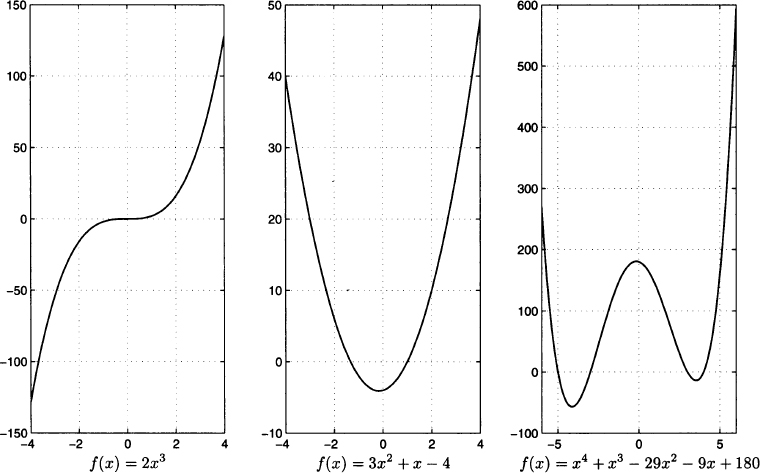
Fig. 2.8 Graphs of polynomial functions.

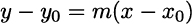
or