Linear Flow of Slightly Compressible Fluids, Steady State

The equation for flow of slightly compressible fluids is modified from what was just derived in the previous section, since the volume of slightly compressible fluids increases as pressure decreases. Earlier in this chapter, Eq. (8.3) was derived, which describes the relationship between pressure and volume for a slightly compressible fluid. The product of the flow rate, defined in STB units, and the formation volume factor have similar dependencies on pressure. The product of the flow rate is given by

where q_R is the flow rate at some reference pressure, p_R. If Darcy’s law is written for this case, with variables separated and the resulting equation integrated over the length of the porous body, then the following is obtained:

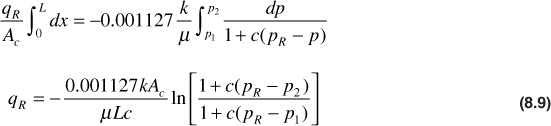
This integration assumes a constant compressibility over the entire pressure drop. For example, under a pressure differential of 100 psi for a permeability of 250 md, a fluid viscosity of 2.5 cp, a length of 450 ft, a cross-sectional area of 45 sq ft, and a constant compressibility of 65(10^–6) psi^–1, choosing p₁ as the reference pressure, the flow rate is

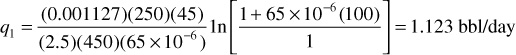
When compared with the flow rate calculation in the preceding section, q₁ is found to be different due to the assumption of a slightly compressible fluid in the calculation rather than an incompressible fluid. Note also that the flow rate is not in STB units because the calculation is being done at a reference pressure that is not the standard pressure. If p₂ is chosen to be the reference pressure, then the result of the calculation will be q₂, and the value of the calculated flow rate will be different still because of the volume dependence on the reference pressure:

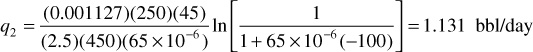
The calculations show that q₁ and q₂ are not largely different, which confirms what was discussed earlier: the fact that volume is not a strong function of pressure for slightly compressible fluids.