Linear combinations

The two basic operations on vectors, addition and multiplication by a scalar, can be combined at wish, resulting in a vector; this is called a linear combination of vectors. The linear combination of vectors v_j with coefficients α_j,

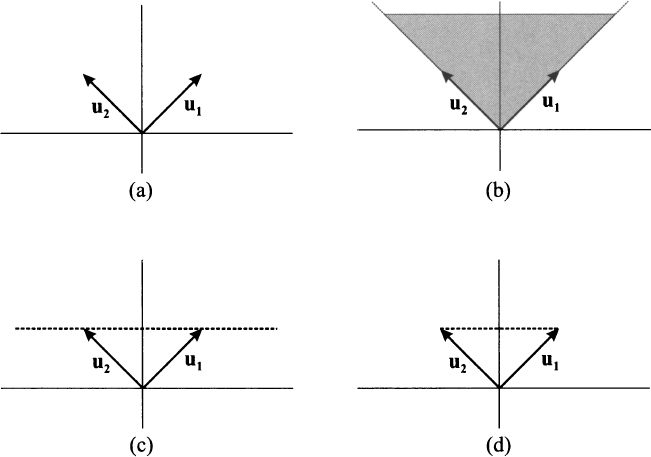
Fig. 3.8 Illustrating linear combinations of vectors.

j = 1, …, m is

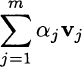
If we denote each component i, i = l, …, n, of vector j by v_ij, the component i of the linear combination above is simply

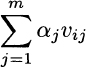
It is useful to gain some geometric intuition to shed some light on this concept. Consider vectors u₁ = [1, 1]^T and u₂ = [−1, 1]^T, depicted in Fig. 3.8(a), and imagine taking linear combinations of them with coefficients α₁ and α₂

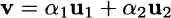
Which set of vectors do we generate when the two coefficients are varied? Here are a few examples:

The reader is strongly urged to draw these vectors to get a feeling for the geometry of linear combinations. On the basis of this intuition, we may try to generalize a bit as follows:

• It is easy to see that if we let α₁ and α₂ take any possible value in , we generate any vector in the plane. Hence, we span all of the two-dimensional space  by expressing any vector as a linear combination of u₁ and u₂.
• If we enforce the additional restriction α₁, α₂ ≥ 0, we take positive linear combinations. Geometrically, we generate only vectors in the shaded region of Fig. 3.8(b), which is a cone.
• If we require α₁ + α₂ = 1, we generate vectors on the horizontal dotted line in Fig. 3.8(c). Such a combination is called affine combination. Note that in such a case we may express the linear combination using one coefficient α as αu₁ + (1 − α)u₂. We get vector u₁ when setting α = 1 and vector u₂ when setting α = 0.
• If we enforce both of the additional conditions, i.e., if we require that weights be nonnegative and add up to one, we generate only the line segment between u₁ and u₂. Such a linear combination is said a convex combination and is illustrated in Fig. 3.8(d).¹⁴