The air standard Brayton cycle or Joule cycle is most ideal thermodynamic cycle for a simple gas turbine plant. Its working is shown in Figure 5.19. Atmospheric air is compressed from pressure P1 to a high pressure P2 in the compressor and delivered to the combustion chamber where fuel is injected and burnt. The combustion process occurs nearly at constant pressure. During combustion heat is added to the working fluid and its temperature rises from T2 to T3. The product of combustion is expanded in the turbine from pressure P3 to atmospheric pressure and discharged into the atmosphere. The turbine and compressor are mechanically coupled to each other; hence the net work is the difference between turbine work and compressor work.
Actual gas turbine cycle is an open cycle; therefore, fresh air must be continuously introduced into the compressor. In closed cycle gas cycle turbine, heat is added by an indirect method, called heat exchanger so that there is no mixing of fuel and air. Similarly, the heat is rejected in another heat exchanger called cooler.
In ideal diagram of Joule cycle, the cycle is assumed to be closed one and heat addition and rejection are only the heat transfer processes at constant pressure. The Joule cycle is shown on P–V and T–s diagram in Figure 5.20.
The various processes are as follows:
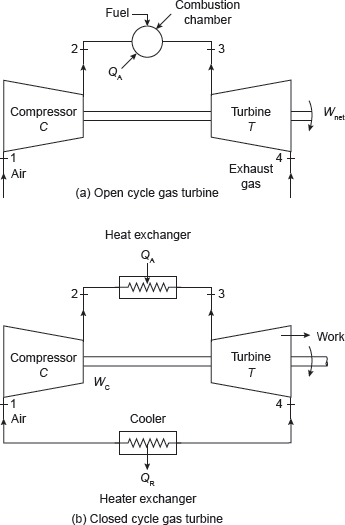
Figure 5.19 Flow Diagram of Turbines
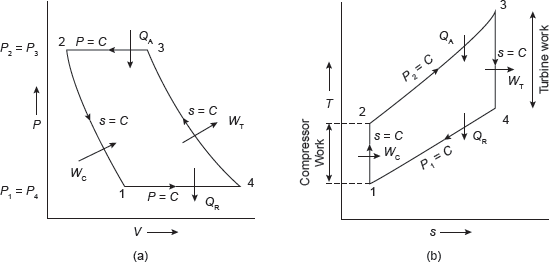
Figure 5.20 ρ−V and T−s Diagrams for Joule Cycle
Process 1–2: Isentropic compression in the compressor thus raising pressure and temperature from P1, T1 to P2, T2.
Process 2–3: Addition of heat at constant pressure raising temperature from T2 to T3.
Process 3–4: Isentropic expansion of air from high pressure and temperature to low pressure and temperature and thus doing work.
Process 4–1: Rejection of heat at constant pressure to restore the original state of air.
Heat addition in Combustion Chamber (CC)
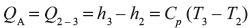
Heat rejection from cooler
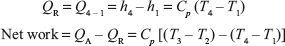
Net work can also be found as
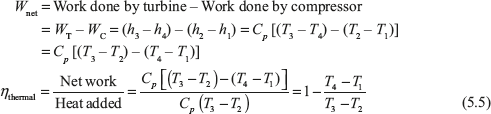
Now, consider Process 1–2
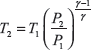
From isentropic expansion Process 3–4
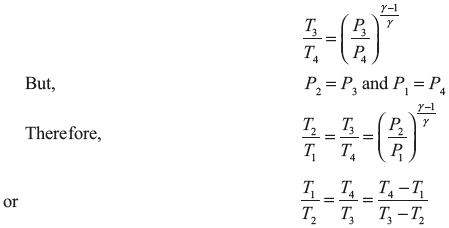
Putting the value of ![]() in Eq. (5.5), we get
in Eq. (5.5), we get

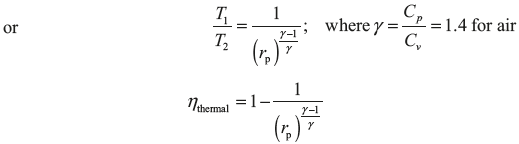
Hence, we can say that the thermal efficiency progressively increases with increasing value of pressure ratio.
Leave a Reply