Isothermal Compressibility

The isothermal compressibility for a substance is given by the following equation:

where

c = isothermal compressibility

V = volume

p = pressure

The equation describes the change in volume that a substance undergoes during a change in pressure while the temperature is held constant. The units are in reciprocal pressure units. When the internal fluid pressure within the pore spaces of a rock, which is subjected to a constant external (rock or overburden) pressure, is reduced, the bulk volume of the rock decreases while the volume of the solid rock material (e.g., the sand grains of a sandstone) increases. Both volume changes act to reduce the porosity of the rock slightly, of the order of 0.5% for a 1000-psi change in the internal fluid pressure (e.g., at 20% porosity to 19.9%).

Studies by van der Knaap indicate that this change in porosity for a given rock depends only on the difference between the internal and external pressures and not on the absolute value of the pressures.⁴ As with the volume of reservoir coils above the bubble point, however, the change in pore volume is nonlinear and the pore volume compressibility is not constant. The pore volume compressibility (c_f) at any value of external-internal pressure difference may be defined as the change in pore volume per unit of pore volume per unit change in pressure. The values for limestone and sandstone reservoir rocks lie in the range of 2 × 10^–6 to 25 × 10^–6 psi^–1. If the compressibility is given in terms of the change in pore volume per unit of bulk volume per unit change in pressure, dividing by the fractional porosity places it on a pore volume basis. For example, a compressibility of 1.0 × 10^–6 pore volume per bulk volume per psi for a rock of 20% porosity is 5.0 × 10^–6 pore volume per pore volume per psi.

Newman measured isothermal compressibility and porosity values in 79 samples of consolidated sandstones under hydrostatic pressure.⁵ When he fit the data to a hyperbolic equation, he obtained the following correlation:

This correlation was developed for consolidated sandstones having a range of porosity values from 0.02 < φ < 0.23. The average absolute error of the correlation over the entire range of porosity values was found to be 2.60%.

Newman also developed a similar correlation for limestone formations under hydrostatic pressure.⁵ The range of porosity values included in the correlation was 0.02 < φ < 0.33, and the average absolute error was found to be 11.8%. The correlation for limestone formations is as follows:

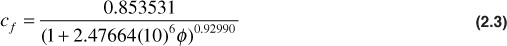
Even though the rock compressibilities are small figures, their effect may be important in some calculations on reservoirs or aquifers that contain fluids of compressibilities in the range of 3 to 25(10)^–6 psi^–1. One application is given in involving calculations above the bubble point. Geertsma points out that when the reservoir is not subjected to uniform external pressure, as are the samples in the laboratory tests of Newman, the effective value in the reservoir will be less than the measured value.⁶