Next time you turn on an electric oven, pay attention to the way in which the color of its glow changes as it heats up. The glow is at first weak and dull red before it turns bright orange. At higher temperatures, such as those in a blacksmith’s metalworking oven, the glow becomes much brighter and whiter.
All materials emit electromagnetic radiation with a very similarly colored glow as a function of temperature. To simplify the study of this phenomenon, physicists make use of an idealized object known as a blackbody. This theoretical device is able to absorb all electromagnetic radiation that reaches it, and then re-emits this radiation in a characteristic, continuous spectrum. Because this object reflects no electro-magnetic radiation (including visible light) it theoretically appears black when it is cold, and this is where it gets its name. However, at any temperature above absolute zero, the blackbody emits a temperature-dependent radiation known as blackbody radiation.
In 1905, British Nobel laureate Lord Rayleigh (his real name was John William Strutt) and his colleague Sir James Jeans derived an expression for blackbody radiation. They assumed that blackbodies are made of a huge number of harmonic oscillators—imaginary contraptions somewhat like guitar strings that can vibrate in response to a sound and can themselves produce a sound when they vibrate.
As shown in Figure 20a, a harmonic oscillator—such as an ideal elastic string held between two walls (which force zero movement at the ends)—is able to vibrate at any wavelength where the string’s ends become zeros of the wave. The frequency of the vibration with the longest wavelength is called the fundamental, and its integer multiples are called harmonics or overtones.
Figure 20 In 1905, Rayleigh and Jeans derived an expression for the blackbody radiation. (a) They assumed that the blackbody is composed of a huge number of electromagnetic harmonic oscillators—somewhat similar to guitar strings—that can support vibrations of any wavelength that fits completely between their two ends. (b) Although the Rayleigh–Jeans expression matches experimental data at low frequencies, it incorrectly predicts infinitely large amounts of radiation at high frequencies.
The classical physics* used by Rayleigh and Jeans requires all harmonic oscillations from a system at equilibrium (one where the energy being gained by the system equals the energy lost by the system) to have an average that is proportional to the system’s temperature. Since there are an infinite number of possible harmonics, this means that the energy of each harmonic must be the same.
Unfortunately, this requirement of classical physics also means that most of the harmonic oscillators will be buzzing along at the smaller wavelengths (which correspond to higher frequencies), where most of the infinite harmonics exist. As a consequence of this, the Rayleigh–Jeans expression predicts an energy output from the blackbody that rises toward infinity as the wavelength approaches zero (Figure 20b).
Since the whole universe is not scorched to a crisp every time we light the oven to bake cookies, something must be terribly amiss with the assumptions made by classical physics regarding the behavior of blackbodies! Einstein, Rayleigh, and Jeans understood this to be a problem that required a breakthrough idea. The failure of early twentieth-century physics to explain blackbody radiation became known as the “Ultraviolet Catastrophe,” since it is obvious that the major discrepancy between theory and experiment occurs at the short wavelengths of the UV.
Let’s see how a blackbody actually radiates as a function of temperature. For this experiment, the filament inside a flashlight bulb will serve as a blackbody that can be safely heated in a controlled manner up to quite high temperatures.
Our experimental setup is shown in Figure 21. We constructed a goniometer stand by cutting in half a wooden metric ruler (these are sold by educational supply stores). We then attached the two halves to a steel protractor, and reinforced the pivot axis with duct tape. We used low-cost optical component holders from a student optical bench sold by Anchor Optics as model AX26095.
Figure 21 Studying the radiation produced by a blackbody is possible using a simple goniometer setup that uses a glass prism to separate light from the blackbody into its component color spectrum (a), (b) The filament of a flashlight lightbulb acts as the blackbody. (c) A low-cost, integrated light-to-voltage converter is used to measure the light intensity at various wavelengths.
A 14-V 200-mA #1487 screw-base flashlight lamp (RadioShack 272-1134) sits on a mating base (RadioShack 272-356) within a 2-in. schedule 40 PVC pipe cap as shown in Figure 2b. A small hole through the cap (e.g., 3/32-in. diameter) provides a direct view to the lamp’s filament. The lamp is powered by a low-voltage, variable, and metered power supply. Light from the lamp assembly is projected by a double-convex lens onto a 30-mm glass equilateral prism (Anchor Optics AX27689), which disperses the light into its constituent colors. The spectrum is focused by a second double-convex lens to form a sharp “rainbow” line at the input slit of the light detector.
We measure light intensity with the same integrated light sensor as we did in chapter 1 for the interference-pattern scanner (Figure 5). The device we use is a TAOS TSL254R-LF light-to-voltage converter. This device is an inexpensive component that incorporates a light-sensitive diode and amplifier on a single chip. It is very easy to use. It requires a supply voltage in the range of 2.7 to 5.5 V (we use two 1.5-V AA batteries in series), and produces an output voltage that is directly proportional to the light intensity (Figure 22a). As shown in Figure 21c, we placed the sensor’s lens behind a small hole that we drilled on a 1 1/4-in. copper pipe cap. We also drilled and tapped two small holes on the sides of the center hole to accept two 2–56 machine screws. These hold two single-edge razor blades that form a slit allowing only a narrow portion of the light spectrum to enter the sensor. We closed the other end of the copper cap with copper tape to ensure that light enters the assembly only through the slit between the two razor blades. We found that adding a bit of matte-finish transparent adhesive tape (Scotch® Matte Finish Magic™ Tape) over the slit improves measurements by diffusing the light before it reaches the sensor’s lens.
Figure 22 The TAOS TSL254R-LF is a light-to-voltage converter that produces an output voltage directly proportional to the light intensity entering through its integrated lens. (a) Power in the range of 2.7–5.5 V is supplied between pin 2 and ground. (b) The output at pin 3 is a voltage that is proportional to light intensity at a rate of 9 mV/(μW/cm2) at λ = 635 nm. The responsivity must be corrected based on this graph for other wavelengths.
None of the components are critical, so you may adapt the design in any way you see fit. The characteristic change in color of the light emitted by a blackbody can be seen by simply varying the supply voltage to the lightbulb. At some point, the filament is hot enough to produce a soft, dull red glow. As the supply voltage is increased, the filament glows brighter, with a more red-orange hue. At even higher voltage, the filament produces intense white light.
The filament is made of tungsten—a metal that has the highest melting point of all the nonalloyed metals. The electrical resistance of tungsten varies with temperature, so we can calculate the filament’s temperature T by monitoring the power supply’s voltage V and current I to measure its resistance when hot:
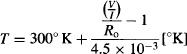
where Ro is the resistance of the filament that you’ll need to measure very carefully with a multimeter at room temperature (around 300° K).
Place a white sheet of paper at the distant end of the goniometer arm opposite where you will place the light sensor. With the bulb shining brightly, adjust the prism, goniometer angle, and location of the lenses to produce a crisp light spectrum. Dim the room lights and vary the lightbulb voltage. Do you see how the short-frequency wavelengths (green, blue, violet) disappear as the voltage is lowered?
Write down the angle of the protractor at which each color falls on the sensor’s slit. The sensor’s range is wider than the spectrum visible to the human eye, so you can take an IR measurement below the lowest red you can see, as well as a UV measurement beyond the deepest visible violet. Equip yourself with a small flashlight and turn off the room lights. Read the light intensity for every color (be consistent with the angle between measurements) at a few different filament voltages.
The voltage output of the TSL254R-LF varies with wavelength, so before you plot your data, correct it according to the sensor responsivity curve of Figure 22b. For example, the measurement for the intensity of light at 850 nm (IR) should be divided by 1.2 to represent the same voltage output per corresponding light intensity as a measurement made at 600 nm (orange). Our results are shown in Figure 23, and show the characteristic distribution that puzzled early twentieth-century physicists.
Figure 23 Blackbody radiation measured with the setup of Figure 21 at three filament voltages.
In 1893, German physicist Wilhelm Wien noted that the wavelength distribution of the radiation from a blackbody at any temperature has essentially the same shape as the distribution at any other temperature, except that each wavelength moves over on the graph. Wien demonstrated that the peak of the spectrum of the light emitted by a blackbody occurs at a wavelength:
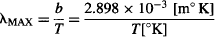
where T is the absolute temperature of the blackbody, and b is Wien’s displacement constant, equal to 2.898 × 10−3 m° K. Wien also came up with an empirical formula for the blackbody spectrum. Although his equation does follow quite closely the shape of the spectrum at short wavelengths, it fails to accurately fit the experimental data for long-wavelength emissions.
Leave a Reply