Incorporating a Flow Equation into the Model

The procedure mentioned in the previous section yields oil and gas production as a function of the average reservoir pressure, but it does not give any indication of the time required to produce the oil and gas. To calculate the time and rate at which the oil and gas are produced, a flow equation is needed. It was found that most wells reach the pseudosteady state after flowing for a few hours to a few days. An assumption will be made that the well used in the history match described in this has been produced for a time long enough for the pseudosteady-state flow to be reached. For this case, Eq. (8.45) can be used to describe the oil flow rate into the wellbore:

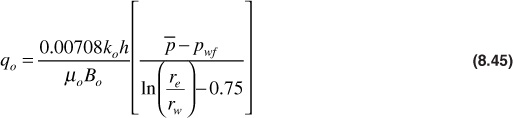
This equation assumes pseudosteady-state, radial geometry for an incompressible fluid. The subscript, o, refers to oil, and the average reservoir pressure, , is the pressure used to determine the production, N_p, in the Schilthuis material balance equation. The incremental time required to produce an increment of oil for a given pressure drop is found by simply dividing the incremental oil recovery by the rate computed from Eq. (8.45) at the corresponding average pressure:

The total time that corresponds to a particular average reservoir pressure can be determined by summing the incremental times for each of the incremental pressure drops until the average reservoir pressure of interest is reached.

Since Eq. (12.2) requires ΔN_p and the Schilthuis equation determines ΔN_p/N, N, the initial oil in place, must be estimated. It was shown that the initial oil in place could be estimated from the volumetric approach by the use of the following equation:

Combining these equations with the solution of the Schilthuis material balance equation yields the necessary production rates of both oil and gas.