So far, we have considered the integral of a continuous function on a bounded interval. The idea can be generalized to unbounded intervals and to functions featuring certain types of discontinuity. In fact, the integral might not exist, because the function has pathological behavior; in other cases, it could go to infinity, which may well be the case if we consider an infinite area. Still, in some fortunate cases we do find an integral that should be regarded as the limit of an integral of a continuous function on a bounded interval. We illustrate the concept with a couple of examples, without providing adequate theoretical background.
Example 2.43 Consider the exponential function f(x) = λe−λx, where λ > 0, and the improper integral
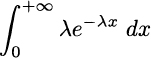
on the unbounded interval [0, +∞). This should be regarded as the following limit:
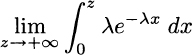
Since the antiderivative of f is F(x) = −e−λx, all boils down to the following calculation:
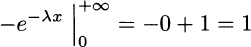
In this case, the integral exists because the negative exponential function goes to zero fast enough, when x → +∞, so that the area on the unbounded interval is still finite. Clearly, the improper integral on the interval (−∞, 0] cannot exist, since the positive function goes to infinity there.
Example 2.44 Consider the definite integral
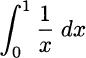
Unlike the previous case, the integration interval is finite here, but the function is not continuous for x = 0 and it goes to +∞. We could still wonder whether the area is finite or, more precisely, whether the limit
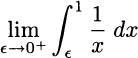
exists. The antiderivative we need is F(x) = lnx. Unfortunately, if we try using it, we fail, since
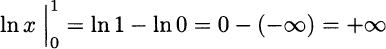
The area is unbounded, as 1/x goes to infinity too quickly. The trick, however, works for 
. In this case, the antiderivative is 
and the integral is
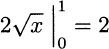
The rate of increase of function g, when x → 0+, is slow enough to result in a finite area.
Leave a Reply