The Bohr atom gave physicists a wonderful basis upon which to visualize and interpret the inner workings of the hydrogen atom. To explore this further, we would benefit from a system to keep track of all the stationary states and energy levels we’ll encounter. To do so, Bohr introduced a counting system based on what he called the quantum number.
ATOM TRAP
Here we are using the concept of quantum number as defined and used in Bohr’s model. In this case, there is exactly one stationary state (and corresponding energy level) per quantum number. However that for a three-dimensional system like the atom, three different quantum numbers are needed to tell the whole story. (Truth be told, the number is four, but now we’re really getting ahead of ourselves).
It’s simple. The ground state is given quantum number 1, and it corresponds to the electron orbit with an angular momentum of 1 quantum (i.e., 1 unit of Planck’s constant divided by 6.28, or h ÷ 2π). Quantum number 2 belongs to the first excited state, which has an angular momentum of 2 quanta. Quantum number 3 corresponds to the second excited state, with 3 quanta. And so it goes, upward to arbitrarily high quantum numbers.
ATOM TRAP
In his semi-quantum treatment, Bohr made a great advance with his quantization of angular momentum and the use of quantum numbers. However, that a full quantum treatment of the hydrogen atom reveals that the ground state actually has zero angular momentum. Never fear, though, the fact that higher energy states have higher amounts of angular momentum will continue to be true.
The next useful concept that Bohr introduced was that of the quantum jump. This is a pithy way of describing the “passing” of an atom from one stationary state to another. As we’ve already mentioned, this is the basis for the atom’s interaction with light. When the electron jumps from a higher energy level to a lower energy level, the atom itself loses energy. We know that the total energy is conserved, however, so the lost energy must have been converted into another form. In this case, it was converted to electromagnetic radiation and carried away by a photon.
In principle, an atom can jump between any arbitrary pair of stationary states. When it does, it emits a photon whose energy equals the difference between the two respective energy levels. This is the basis of the discrete line spectrum, where each spectral line is tied back to the difference between a particular pair of energy levels. Since the spacing of each atom’s energy levels is unique, each atom has its own unique line spectrum. Also, since there is no theoretical limit to the number of possible energy levels, atomic spectra can contain a great many lines spanning a great range of frequencies.
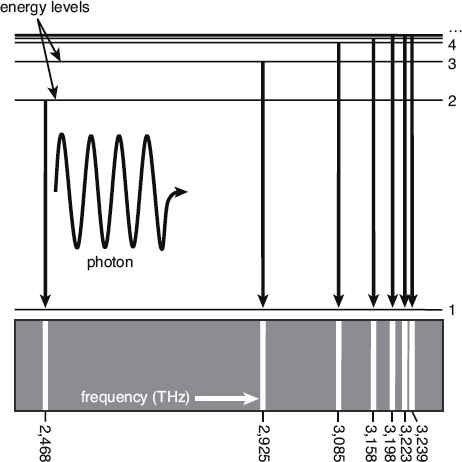
This is a schematic representation of the first few energy levels of hydrogen, and the corresponding spectral lines for transitions to the ground state. When the electron makes a quantum jump from an excited state to the ground state, one photon is emitted. The numbers on the right are the quantum numbers.
Though illustrative, the term quantum jump is actually a little bit misleading. If an electron were really to take off from one orbit and then travel inward to another, it would necessarily radiate (and lose) energy while en route. Since this is counter to observation, there must be another explanation.
DEFINITION
Quantum numbers are assigned to an atom’s stationary states, with the ground state being number 1 and each successive excited state taking the numbers 2, 3, 4, and so on.
A quantum jump is an atomic transition from one stationary state to another. It is accompanied by the emission (or absorption) of a photon, the energy of which exactly matches the difference in corresponding energy levels.
The only interpretation that survives any real scrutiny is that the atom essentially ceases to exist in its initial state and then suddenly begins to exist in the final state! This is a purely quantum effect that is difficult to visualize and which defies a simple physical interpretation based on everyday intuition. It is, however, the way that it is.
Bohr’s model allows us to understand the missing lines in atomic absorption spectra. If a beam of monochromatic light is shone onto an atom, the atom can absorb photons and transition from a lower-lying stationary state to any higher excited state. In this case, the quantum jump is upward, and the final energy level is higher than the initial energy level.
However, this can only occur if two conditions are met. First, the photon energy must exactly match the difference between two of the atom’s energy levels. Second, somewhere in the gas there must be at least one atom in the lower-lying stationary state in the first place. Otherwise, there would be no way for any atoms in the gas to absorb a photon’s energy and make the transition to the excited state.
So how does this explain the discrepancy between emission and absorption lines? Well, emission occurs whenever atoms have been somehow excited. This can occur, for example, when a gas is heated and the atoms collide with one another and absorb some kinetic energy. Once some of the atoms are in excited states, it is just a matter of time before they will de-excite and drop down to lower energy levels, emitting light. Since there is no limitation on which state the atoms can be excited into, nor to which states they can decay, all possible combinations of frequencies are emitted.
If you try to measure absorption by a cold gas, however, you will see fewer spectral lines. This is because the atoms in the cold gas are less energetic, so there are fewer atom-atom collisions and therefore chances are good that none of the atoms will be excited into some of the more energetic stationary states. Any frequency that links one of these “unpopulated,” lower-lying stationary states to more energetic states will therefore be absent in the absorption spectrum.
Finally, it’s worth noting that the spacing between energy levels gets smaller and smaller for larger and larger quantum numbers. They are not equally spaced as they were in Planck’s blackbody. For infinitely large quantum numbers, the spacing between atomic energy levels shrinks to essentially zero. This implies that there is an upper limit for the highest possible energy level, which physicists refer to as the threshold.
If an atom absorbs a photon with energy exceeding the difference between the initial energy level and the threshold, the electron will actually be knocked right out of the atom. The “excess” energy will then be transferred to the ejected electron in the form of kinetic energy. This, of course, is the basis of the photoelectric effect.

NIELS BOHR
Born in Copenhagen in 1885, Niels Bohr was earning his driver’s license right about the time Max Planck discovered the quantum of action. Bohr went on to earn significantly more, such as the Gold Medal of the Royal Danish Academy of Science and a ticket to work with the great J. J. Thomson at his laboratory in Cambridge.
Bohr’s direct and matter-of-fact nature undermined their first encounter. Though he was certainly only trying to help, Bohr began by pointing out an error in one of Thomson’s. Not surprisingly, the two men got off to a frosty start. It only got worse, and the bad chemistry ultimately drove Bohr to go work under Thomson’s rival, Earnest Rutherford. Here he began his successful quest to quantize the atom, which ultimately confirmed the nuclear theory of Rutherford.
A true pragmatist, Bohr had no qualms with patching together a hodgepodge of various ideas until he cobbled together a solution that worked. With this approach he was remarkably effective beginning, of course, with his atomic model. The Bohr atom, unveiled in a series of 1913 papers that filled a voluminous 69 pages, would earn him yet another accolade: the 1922 Nobel Prize in physics.
During World War II, Bohr was secretly recruited to England to help research the atomic bomb. He initially declined, thinking the device would prove impractical. After he was forced to flee Denmark during the German occupation, the pragmatist changed his mind. He eventually traveled to Los Alamos, where he would assume an important mentorship role in the final years of the Manhattan Project.
Leave a Reply