Consider a hollow sphere of internal radius r1 and external radius r2 as shown in Figure 7.8. Let the inside and outside surface temperature be t1 and t2; and let the thermal conductivity be k. Consider a small element of thickness dr at any radius r. It can be shown that the surface area of this spherical element is given by 4πr2. The heat transfer rate
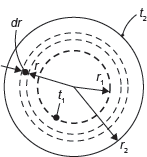
Figure 7.8 Heat Transfer through Sphere
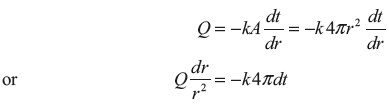
On integrating, we get
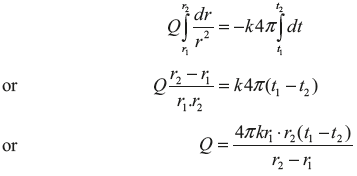
Applying electrical analogy, we get
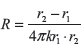
If the concept of mean area, Am and mean radius, rm are applied
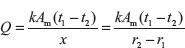
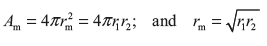
rm is geometric mean.
Example 7.6: A small hemispherical oven is built of an inner layer of insulating firebrick 120 mm thick and an outer covering 80% magnesia 40 mm thick. The inner surface of the oven is 820°C and the heat transfer coefficient for the outside surface is 10 W/m2K; the room temperature is 22°C. Calculate the heat loss through the hemisphere, if the inside radius is 0.8 m. Take the thermal conductivities of firebrick and 80% magnesia as 0.31 and 0.05 W/m K.
Solution:
Given:
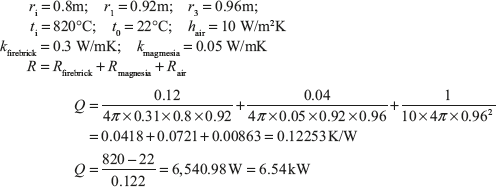
Leave a Reply