The size of a group influences the web of relationships within it. The larger the group, the greater the sets of interpersonal interactions, and the more complicated the nature of its organization. A two-person group has the smallest number of interacting lines. As the size increases, so does the number of relationship structures. Sociometric charts are used to investigate such patterns. Such a dyadic relationship (paired relationships) in any group depends upon the number of persons forming the group. The logically possible dyadic8 relationship in any group can be determined by using the formula:
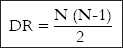
In which N stands for number of people in a group, and DR stands for dyadic relationship.
Consider the mathematical number of relationships among two to seven people …. (T)wo people form a single relationship; adding a third person results in three relationships; adding a fourth person yields six. Increasing the number of people one at a time, then, expands the number of relationships much more rapidly since every new individual can interact with everyone already there. Thus, by the time seven people join one conversation, twenty-one ‘channels’ connect them (Macionis, 2005: 168–69)
To demonstrate this, let us construct a 7 × 7 matrix.
Table 5.1 Mathematical Number of Relationships between Two to Seven People
It will be noticed that on each side of the diagonal are 21 boxes marked with ×—the total number of possible dyadic relationships in a seven-member group. Although one can stretch this and work out such relationships in any size of the group, in reality many of those logical boxes will remain empty in terms of actual interactions. Thus, this technique is employed only for small group research. Diagrammatically, this can be shown below:
Figure 5.2 Group Size and Relationships
Source: Macionis, 2005: 168
Sub-Groups
When a group is created within a group, it becomes a sub-group, and the actions of the members of this sub-group remain primarily oriented towards the main group. The activities carried out within the sub-group are specialized, and are functional for the larger group of which it is a part. But the formal group, particularly the larger one, allows or facil-itates the formation of several small informal groups or friendship circles. In an office, one may notice that during lunch break, a small number of officers of identical9 rank assemble to have lunch together, and share their lunches. The lunch session also gives them an opportunity to engage in conversation on a wide variety of topics, not all necessarily linked to their office. These lunch groups discuss personal and familial problems, national and international affairs, and at times, intellectual topics as well. Thus such a group, composed of the members of a common formal group—a bureaucracy—is not a strict sub-group of the former, but is primarily united by that bond.
When a sub-group becomes self-contained and insulates itself from the main group, it begins to assume the characteristics of a group; when the insulation creates an insurmountable boundary, the original group’s boundaries are also redefined through the exclusion of the portion of insulated boundary of the former sub-group. This can be explained through a Venn diagram.
Suppose there are four groups called A, C, C1 and C2. In order for C1 and C2 to be proper subsets of Group C, it would be necessary for each element of C to also be an element of C1 and C2. In other words, a subset always falls within the boundary of the set. But when a group begins to share the elements of two or more sets, it heralds the beginning of a new formation of the set—as a hybrid progeny. In terms of Set theory, this may be written thus:
Let there be a group called C.
Now C={cl, c2, c3, c4, c5,… ck,… cn}; and
C1={c3, c4, c8, c9, ck}.
In this case, C1 is a subset of C because the elements of C1 are contained in C.
But suppose there is another group, C2, such that it has the following internal structure:
C2={c1, c5, c6, c11}, {c2-1, c2-2, c2-3,…}, {al, a5, a7}
In that case, it may be a breakaway group either of Group A or Group C, trying to move into the other group and deserting the parent group. Such a group is not, strictly speaking, a sub-group of either, but is a processual product of secession and aspiration to join another group, or become marginalized and form a group of its own.
Thus, it emerges that a person can be a member of a number of groups at the same time. Of course, membership to any particular group gets activated when the person participates in that group; otherwise it remains dormant.
Figure 5.3 Rectangle Representing Set C
Figure 5.4 Set C, Set C2, and Set A
Note: C2 is neither a subset of C, nor of A, though some of its members are drawn from C and A respectively. In this case, 1, 5, 6, and 11 of Set C constitutes a subset of C; similarly, 1, 5 and 7 of Set A are a subset of A. But these two subsets, plus the remainders of Set C2, constitute the different set we have called C2..
It should be remembered that such dual membership depends on the kind of groups we are referring to. Some groups allow such dual membership in the same domain. Other groups belonging to different domains, have no problem with multiple memberships. Non-Resident Indians now being granted dual citizenship—that of their country of residence and that of India—offer a good example. Such people are given a PIO (Person of Indian Origin) card or an OCI (Overseas Citizen of India) card.10
Each of us can supply examples of multiple memberships as we all belong to several groups at any given point in time. An individual ‘I’ belongs to her family, her class at school (if the school is treated as a group, then class becomes a sub-group), a playgroup, a political party, and so on. In this sense, an individual is regarded as a bundle of statuses and roles. It is like ‘well-wrapped sliced bread’; while each slice represents a status, the entire piece is identified as bread. Since the statuses remain more or less stationary but their occupants change, sociologists focus on statuses and positions in groups rather than on individuals as analytical categories. The personality of an individual—which is the subject matter of Psychology—is shaped by a person’s participation in various groups.
This brings us to another logical inference. The participation of an individual in any group setting is influenced not only by what happens within the group, but also by the totality of other memberships held by that particular individual. The performance of a player in the field, for example, is not only affected by the attitude and behaviour of others in the team, or the rival team, or field conditions, but also on the other engagements of the player in other groups. If the father of a given player is on his death-bed, the latter’s concentration in the game might naturally be affected. The presence or absence of the player’s sweetheart in the stadium may have an effect on the player’s performance. Thus, other groups vicariously intervene in the functioning of a particular group, and in the participation of its member. When an officer’s behaviour on a given day is somewhat rude, his subordinates might attribute it to a bad start at home—perhaps a quarrel with the wife!
It must be stressed that an individual’s personality is shaped by the kind of statuses he holds and the roles he plays relative to each status.11 In different situations relevant statuses come into play when others become secondary and lie dormant. While playing cricket, for example, Sachin Tendulkar’s image of a master-blaster reigns supreme, while his other statuses as an Indian citizen, a husband, owner of a prestigious restaurant, and so on remain secondary, although not inconsequential; even these statuses, and the roles associated with them, influence this player’s performance on the cricket field. We know that when Sachin was playing cricket in England, he received the news of his father’s death and had to rush back to India to attend the funeral and perform the associated rites. This affected his participation in the game. Playing against Pakistan certainly evokes the Indian-ness in the Indian cricketer, and loyalty towards his country in the Pakistani player. National pride, although not part of the package for the game of cricket, does surreptitiously enter the frame of reference of individual players, and influences their performance in the field.
Hence, a group continues to exist even when its members ‘are not gathered together in the same place, in one another’s physical presence’ (Johnson, 1960: 6).
Membership in different groups gives an individual different statuses. However, any individual is known publicly by one of his statuses, which is called the dominant status. Taking the example of a cricketer, we can say that M. S. Dhoni or Sachin Tendulkar is known primarily as a cricketer representing India. Their other membership statuses remain somewhat subdued. Sonia Gandhi is known as the President of the Congress Party, and Lal Krishna Advani as a BJP leader. The heir-apparent of a Maharana is known as Kunwar Sahib.
The dominant status affects the participation of individuals in other groups; however, these other memberships are regarded as secondary to the principal (or dominant) status.
SUMMARY
Let us summarize the main points that emerged from the preceding discussion:
- Although a group consists of people, in sociological terms it ‘consists of certain persons in their capacity as members’ For example, a cricketer is not just a player; he belongs to a family, a religious group, a school, a country, an official in a corporate group (for example, Rahul Dravid is an employee of the Bank of Baroda), he participates in many friendships, clubs, or neighbourhood activities. His/her action in all these groups is not part of his/her participation in the cricket team. However, any individual is a well-integrated personality, and his various memberships affect his performance, behaviour, sub-group formation, etc., in different settings.
- A group does not cease to exist when its members leave one another temporarily. The departure of certain members—due to death or migration or resignation—may change the profile of the group, but does not threaten its existence.
- The group, understood as a ‘social system’, is a system of interaction, different from groups understood as an aggregate of persons.
- The same criteria may be applied to distinguish between a group and a sub-group. A sub-group is a subset within the group, but is carved out in terms of certain specific attributes—older versus younger members, male and female members, etc.
- The members of a social system are differentiated according to the social positions they occupy. A social position is a complex of rights and obligations. A person is said to ‘occupy’ a ‘position’ if s/he has a certain cluster of obligations and enjoys a certain cluster of associated rights within a social system. These are known as role (referring to obligations) and status (referring to rights). The role structure of a group is the same as its status structure, because a role from the point of view of one member is actually status from the point of view of others.
- A group should be differentiated from ‘Alliances’ and Networks’. An alliance may be a group of groups, where constituents maintain their individual identities and yet agree to cooperate with other alliance members on a commonly agreed agenda. A network, on the other hand, constitutes the totality of social relationships of an individual or a group vis-à-vis other individual/s or groups in a given context. There will be several occasions in the course of our understanding of social systems to explicate these distinctions further.
Leave a Reply