Generalized Vogel Inflow Performance

If the reservoir pressure is above the bubble point and yet the flowing bottomhole pressure is below, a generalized inflow performance can be written. The following approach enables generation of an IPR that has a straight portion for p_wf ≥ p_b, and follows the Vogel equation for p_wf < p_b adapted to the straightforward logic found in Standing (1971). This can be done for transient, steady state, and pseudosteady state. First, q_b, the flow rate where p_wf = p_b, can be written as

where p_D is the transient dimensionless pressure drop or is equal to ln(r_e/r_w) for steady state or ln(0.472 r_e/r_w) for pseudosteady state.

The productivity index above the bubble point is simply

and is related to q_v (denoted here as “Vogel” flow, q_V) by

For p_wf ≥ p_b,

For p_wf < p_b,

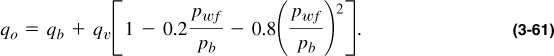
When  is less than or equal to the original bubble-point pressure, use Equation 3-55.