Gas Formation Volume Factor

The formation volume factor relates the reservoir volume to the volume at standard conditions of any hydrocarbon mixture. In the case of a natural gas, the formation volume factor, B_g, can be related with the application of the real gas law for reservoir conditions and for standard conditions. Thus,

For the same mass, nR can be cancelled out and, after substitution of Z_sc ≈ 1, T_sc = 60 + 460 = 520°R, and p_sc = 14.7 psi, Equation (4-27) becomes

---

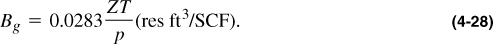
Example 4-5. Initial Gas-in-Place

Calculate the initial gas-in-place, G_i, in 1900 acres of the reservoir described in Appendix C. Properties are also listed in Appendix C.

Solution

The initial formation volume factor, B_gi, is given by Equation (4-28) and therefore

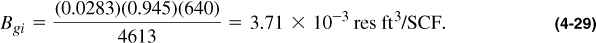
Then

and

---

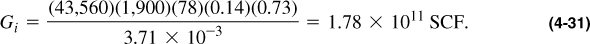
Gas Isothermal Compressibility

The gas compressibility, c_g, often referred to as isothermal compressibility, has an exact thermodynamic expression:

For an ideal gas, it can be shown readily that c_g is exactly equal to 1/p. For a real gas, using Equation (4-2), the derivative ∂V/∂p can be evaluated:

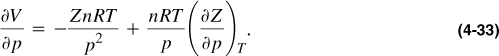
Substitution of the volume, V, by its equivalent from Equation (4-2) and the derivative ∂V/∂p from Equation (4-33) into Equation (4-32) results in

or, more conveniently, remembering the relationship between pseudoreduced and pseudocritical pressure (Equation 4-3),

Equation (4-35) is useful because it allows the calculation of the compressibility of a real gas at any temperature and pressure. Needed are the gas compressibility factor Z and the slope of the Standing-Katz correlation, ∂Z/∂p_pr, at the corresponding temperature (i.e., the associated pseudoreduced temperature curve). The slope can be determined by differentiating Equation 4-35 with respect to the pseudoreduced pressure holding the temperature constant.