Hydrodynamically, there are two types of fluid flow: laminar and turbulent. Whether a flow is viscous or turbulent can be decided by the Reynold’s number RD. If RD > 2,000, the flow is turbulent otherwise laminar. In the present case we will assume that the flow is turbulent, that is the normal case for practical situations. Let us consider the fluid flow through a closed channel of variable cross-section, as shown in Figure 18.6. Let the pressure, velocity, cross-sectional area, and height above the datum be expressed as p1, v1, A1, and z1 for section 1 and the corresponding values for section 2 be p2, v2, A2, and z, respectively. We also assume that the fluid flowing is incompressible.
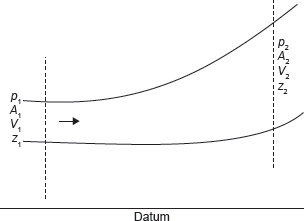
Figure 18.6 Turbulent Flow through a Channel
From Bernoulli’s equation
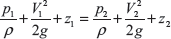
where ρ is the specific weight of the fluid.
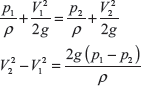
Since flow is incompressible, hence v = A1V1 = A2V2 ⇒ V1/V2 = A2/A1
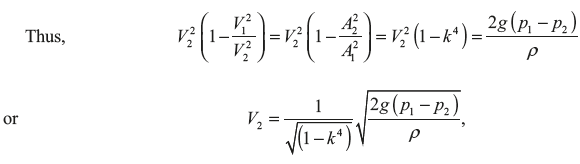
where k is ratio of diameters at section 2 and 1; i.e. k = d2/d1.
Volume of flow,
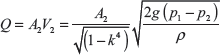
Leave a Reply