The developers of the Apache Commons Lang framework (the framework where I extracted the implementation of the substringsBetween method) are just too good. We did not find any bugs there. Let’s look at another example: one implemented by me, an average developer who makes mistakes from time to time. This example will show you the value of specification testing. Try to spot the bug before I reveal it!
Some friends and I have participated in many coding challenges, primarily for fun. A couple of years ago we worked on the following problem inspired by LeetCode (https://leetcode.com/problems/add-two-numbers):
The method receives two numbers, left and right (each represented as a list of digits), adds them, and returns the result as a list of digits.
Each element in the left and right lists of digits should be a number from [0–9]. An IllegalArgumentException is thrown if this pre-condition does not hold.
left—A list containing the left number. Null returnsnull; empty means 0.right—A list containing the right number. Null returnsnull; empty means 0.
The program returns the sum of left and right as a list of digits.
For example, adding the numbers 23 and 42 means a (left) list with two elements [2,3], a (right) list with two elements [4,2] and, as an output, a list with two elements [6,5] (since 23 + 42 = 65).
My initial implementation was as follows.
Listing 2.9 Initial implementation of the add() method
public List<Integer> add(List<Integer> left, List<Integer> right) {
if (left == null || right == null) ❶
return null;
Collections.reverse(left); ❷
Collections.reverse(right);
LinkedList<Integer> result = new LinkedList<>();
int carry = 0;
for (int i = 0; i < max(left.size(), right.size()); i++) { ❸
int leftDigit = left.size() > i ? left.get(i) : 0;
int rightDigit = right.size() > i ? right.get(i) : 0;
if (leftDigit < 0 || leftDigit > 9 ||
rightDigit < 0 || rightDigit > 9) ❹
throw new IllegalArgumentException();
int sum = leftDigit + rightDigit + carry; ❺
result.addFirst(sum % 10); ❻
carry = sum / 10; ❼
}
return result;
}❶ Returns null if left or right is null
❷ Reverses the numbers so the least significant digit is on the left
❸ While there is a digit, keeps summing, taking carries into consideration
❹ Throws an exception if the pre-condition does not hold
❺ Sums the left digit with the right digit with the possible carry
❻ The digit should be a number between 0 and 9. We calculate it by taking the rest of the division (the % operator) of the sum by 10.
❼ If the sum is greater than 10, carries the rest of the division to the next digit
The algorithm works as follows. First it reverses both lists of digits, so the least significant digit is on the left. This makes it easier for us to loop through the list. Then, for each digit in both the left and right numbers, the algorithm gets the next relevant digits and sums them. If the resulting sum is greater than 10, +1 needs to be carried to the next most significant digit. In the end, the algorithm returns the list.
I was just having fun with coding, so I did not write systematic tests. I tried a couple of inputs and observed that the output was correct. If you already understand the concept of code coverage, these four tests achieve 100% branch coverage if we discard the ifs related to checking null and pre-conditions:
- T1 = [1] + [1] = [2]
- T2 = [1,5] + [1,0] = [2,5]
- T3 = [1,5] + [1,5] = [3,0]
- T4 = [5,0,0] + [2,5,0] = [7,5,0]
The program worked fine for these inputs. I submitted it to the coding challenge platform, and, to my surprise, the implementation was rejected! There was a bug in my code. Before I show you where it is, here is how specification testing would have caught it.
First we analyze each parameter in isolation:
leftparameter —It is a list, so we should first exercise basic inputs such as null, empty, a single digit, and multiple digits. Given that this list represents a number, we should also try a number with many zeroes on the left. Such zeroes are useless, but it is good to see whether the implementation can handle them. Thus we have the following partitions:rightparameter —We have the same list of partitions as for theleftparameter:
left and right have a relationship. Let’s explore that:
While not explicit in the documentation, we know that the sum of two numbers should be the same regardless of whether the highest number is on the left or right side of the equation. We also know that some sums require carrying. For example, suppose we’re summing 18 + 15: 8 + 5 = 13, which means we have a 3, and we carry +1 to the next digit. We then add 1 + 1 + 1: the first 1 from the left number, the second 1 from the right number, and the third 1 carried from the previous sum. The final result is 33. Figure 2.5 illustrates this process.
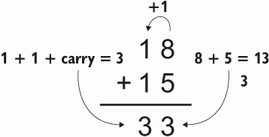
Figure 2.5 Illustrating the carry when summing 18 + 15
The carry is such an important concept in this program that it deserves testing. This is what I meant in listing 2.9 when I said to pay extra attention to specific (business) rules and logic:
Domain knowledge is still fundamental to engineer good test cases
Up to this point may have given you the impression that if you analyze every parameter of the method, you can derive all the test cases you need. Life would be much easier if that were true!
Analyzing parameters, even without much domain knowledge, will help you uncover many bugs. However, having a deep understanding of the requirements is still key in devising good test cases. In the current example, the requirements do not discuss the carry. We devised many tests around the carry because we have a deep knowledge of the problem. We build up knowledge over time; so although the systematic approaches I discuss will help you uncover many common bugs, it is your job to learn about the domain of the software system you’re working on. (And if you wrote the code, you have an advantage: you know it deeply!)
The only boundary worth testing is the following: ensuring that cases such as 99 + 1 (where the final number is carried to a new, most significant digit) are covered. This comes from the last partition derived when analyzing the carry: “Sum with a carry: carry propagated to a new (most significant) digit.”
With all the inputs and outputs analyzed, it is time to derive concrete test cases. Let’s apply the following strategy:
- Test nulls and empties just once.
- Test numbers with single digits just once.
- Test numbers with multiple digits, with
leftandrighthaving the same and different lengths. We will be thorough and have the same set of tests for both equal and different lengths, and we will duplicate the test suite to ensure that everything works ifleftis longer thanrightor vice versa. - We will exercise the zeroes on the left, but a few test cases are enough.
- Test the boundary.
Let’s look at the specific test cases:
- Nulls and empties
- Single digits
- Multiple digits
- Multiple digits with different lengths (one for
leftlonger thanright, and one forrightlonger thanleft) - Zeroes on the left
- Boundaries
Now we transform them into automated test cases, as shown in listing 2.10. A few remarks about this listing:
- This test uses the
ParameterizedTestfeature from JUnit. The idea is that we write a single generic test method that works like a skeleton. Instead of having hard-coded values, it uses variables. The concrete values are passed to the test method later. ThetestCases()method provides inputs to theshouldReturnCorrectResulttest method. The link between the test method and the method source is done through the@MethodSourceannotation. JUnit offers other ways to provide inputs to methods, such as inline comma-separated values (see the@CsvSourceannotation in the documentation). - The
numbers()helper method receives a list of integers and converts it to aList<Integer>, which the method under test receives. This helper method increases the legibility of the test methods. (For the Java experts, theArrays.asList()native method would have yielded the same result.)
Listing 2.10 Tests for the add method
import org.junit.jupiter.params.ParameterizedTest;
import org.junit.jupiter.params.provider.Arguments;
import org.junit.jupiter.params.provider.MethodSource;
import java.util.ArrayList;
import java.util.List;
import java.util.stream.Stream;
import static org.assertj.core.api.Assertions.assertThat;
import static org.assertj.core.api.Assertions.assertThatThrownBy;
import static org.junit.jupiter.params.provider.Arguments.of;
public class NumberUtilsTest {
@ParameterizedTest ❶
@MethodSource("testCases") ❷
void shouldReturnCorrectResult(List<Integer> left,
List<Integer> right, List<Integer> expected) {
assertThat(new NumberUtils().add(left, right)) ❸
.isEqualTo(expected);
}
static Stream<Arguments> testCases() { ❹
return Stream.of(
of(null, numbers(7,2), null), // T1 ❺
of(numbers(), numbers(7,2), numbers(7,2)), // T2 ❺
of(numbers(9,8), null, null), // T3 ❺
of(numbers(9,8), numbers(), numbers(9,8 )), // T4 ❺
of(numbers(1), numbers(2), numbers(3)), // T5 ❻
of(numbers(9), numbers(2), numbers(1,1)), // T6 ❻
of(numbers(2,2), numbers(3,3), numbers(5,5)), // T7 ❼
of(numbers(2,9), numbers(2,3), numbers(5,2)), // T8 ❼
of(numbers(2,9,3), numbers(1,8,3), numbers(4,7,6)), // T9 ❼
of(numbers(1,7,9), numbers(2,6,8), numbers(4,4,7)), // T10 ❼
of(numbers(1,9,1,7,1), numbers(1,8,1,6,1), ❼
numbers(3,7,3,3,2)), // T11 ❼
of(numbers(9,9,8), numbers(1,7,2), numbers(1,1,7,0)), // T12 ❼
of(numbers(2,2), numbers(3), numbers(2,5)), // T13.1 ❽
of(numbers(3), numbers(2,2), numbers(2,5)), // T13.2 ❽
of(numbers(2,2), numbers(9), numbers(3,1)), // T14.1 ❽
of(numbers(9), numbers(2,2), numbers(3,1)), // T14.2 ❽
of(numbers(1,7,3), numbers(9,2), numbers(2,6,5)), // T15.1 ❽
of(numbers(9,2), numbers(1,7,3), numbers(2,6,5)), // T15.2 ❽
of(numbers(3,1,7,9), numbers(2,6,8), numbers(3,4,4,7)), // T16.1 ❽
of(numbers(2,6,8), numbers(3,1,7,9), numbers(3,4,4,7)), // T16.2 ❽
of(numbers(1,9,1,7,1), numbers(2,1,8,1,6,1), ❽
numbers(2,3,7,3,3,2)), // T17.1 ❽
of(numbers(2,1,8,1,6,1), numbers(1,9,1,7,1), ❽
numbers(2,3,7,3,3,2)), // T17.2 ❽
of(numbers(9,9,8), numbers(9,1,7,2), numbers(1,0,1,7,0)), // T18.1 ❽
of(numbers(9,1,7,2), numbers(9,9,8), numbers(1,0,1,7,0)), // T18.2 ❽
of(numbers(0,0,0,1,2), numbers(0,2,3), numbers(3,5)), // T19 ❾
of(numbers(0,0,0,1,2), numbers(0,2,9), numbers(4,1)), // T20 ❾
of(numbers(9,9), numbers(1), numbers(1,0,0)) // T21 ❿
);
}
private static List<Integer> numbers(int... nums) { ⓫
List<Integer> list = new ArrayList<>();
for(int n : nums)
list.add(n);
return list;
}
}❶ A parameterized test is a perfect fit for these kinds of tests!
❷ Indicates the name of the method that will provide the inputs
❸ Calls the method under test, using the parameterized values
❺ Tests with nulls and empties
❽ Tests with multiple digits, different length, with and without carry (from both sides)
❾ Tests with zeroes on the left
⓫ Auxiliary method that produces a list of integers. Auxiliary methods are common in test suites to help developers write more maintainable test code.
Interestingly, a lot of these test cases break! See the JUnit report in figure 2.6. For example, take the first failing test, T6 (single digit with a carry). Given left = [9] and right = [2], we expect the output to be [1,1]. But the program outputs [1]! T12 (“carry propagated to a new (now most significant) digit”) also fails: given left = [9,9,8] and right = [1,7,2], we expect the output to be [1,1,7,0], but it is [1,7,0]. The program cannot handle the carry when the carry needs to become a new leftmost digit.
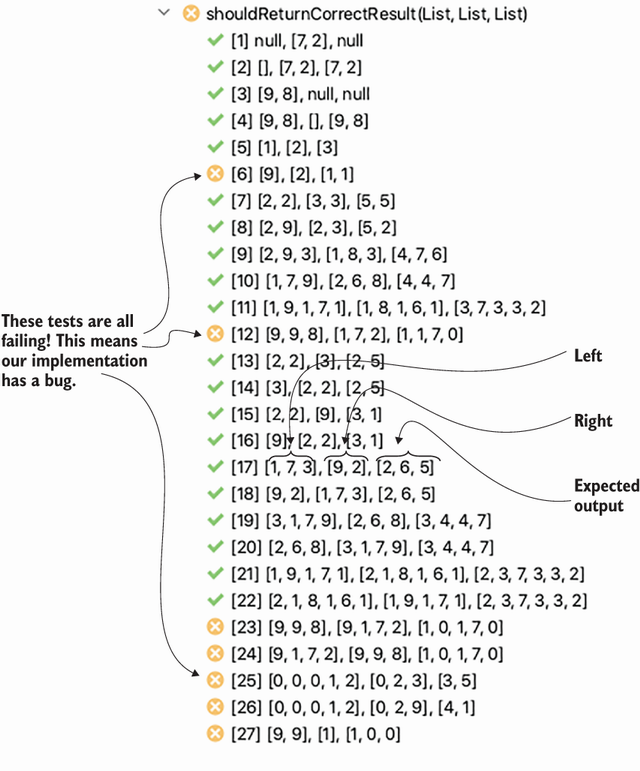
Figure 2.6 The results of the test cases we just created. A lot of them fail, indicating that the program has a bug!
What a tricky bug! Did you see it when we wrote the method implementation?
There is a simple fix: all we need to do is add the carry at the end, if necessary. Here’s the implementation.
Listing 2.11 First bug fix in the add program
// ... all the code here ...
if (carry > 0)
result.addFirst(carry);
return result;With these tests passing, we see that the program does not handle zeroes to the left. When left = [0,0,0,1,2] and right = [0,2,3], we expect the output to be [3,5], but the program returns [0,0,0,3,5]. The fix is also straightforward: remove the zeroes on the left before returning the result (listing 2.12).
Listing 2.12 Second bug fix in the add program
// ... previous code here...
if (carry > 0)
result.addFirst(carry);
while (result.size() > 1 && result.get(0) == 0) ❶
result.remove(0);
return result;❶ Removes leading zeroes from the result
We’re only missing test cases to ensure that the pre-condition holds that each digit is a number between 0 and 9. All we need to do is pass various invalid digits. Let’s do it directly in the JUnit test as follows.
Listing 2.13 Tests for a pre-condition of the add program
@ParameterizedTest ❶
@MethodSource("digitsOutOfRange")
void shouldThrowExceptionWhenDigitsAreOutOfRange(List<Integer> left,
➥ List<Integer> right) {
assertThatThrownBy(() -> new NumberUtils().add(left, right))
.isInstanceOf(IllegalArgumentException.class); ❷
}
static Stream<Arguments> digitsOutOfRange() { ❸
return Stream.of(
of(numbers(1,-1,1), numbers(1)),
of(numbers(1), numbers(1,-1,1)),
of(numbers(1,10,1), numbers(1)),
of(numbers(1), numbers(1,11,1))
);
}❶ A parameterized test also fits well here.
❷ Asserts that an exception happens
All tests are now passing. Given the thoroughness of our test suite, I feel confident enough to move on.
NOTE Interestingly, the bugs we found in this example were caused not by buggy code but by a lack of code. This is a common type of bug, and it can be caught by specification testing. When in doubt, write a test! Writing automated (unit) test cases is so quick that they let you easily see what happens. Having too many useless tests is a problem, but a couple will not hurt.
Leave a Reply