Features of point estimators

We list here a few desirable properties of a point estimator  for a parameter θ. When comparing alternative estimators, we may have to trade off one property for another. We are already familiar with the concept of unbiased estimator. An estimator  is unbiased if

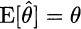
We have shown that sample mean is an unbiased estimator of expected value; in Chapter 10 we will show that ordinary least squares, under suitable hypotheses, yield unbiased estimators of the parameters of a linear statistical model. Biasedness is related to the expected value of an estimator, but what about its variance? Clearly, ceteris paribus, we would like to have an estimator with low variance.

DEFINITION 9.16 (Efficient unbiased estimator) An unbiased estimator  is more efficient than another unbiased estimator  if

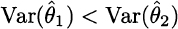
Note that we must compare unbiased estimators in assessing efficiency. Otherwise, we could obtain a nice estimator with zero variance by just choosing an arbitrary constant. It can be shown that, under suitable hypotheses, the variance of certain estimators has a lower bound. This bound, known as the Cramér-Rao bound, is definitely beyond the scope of this book, but the message is clear: We cannot go below a minimal variance. If the variance of an estimator attains that lower bound, then it is efficient. Another property that we have already hinted at is consistency. An estimator is consistent if plim .

Example 9.35 The statistic

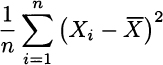
is not an unbiased estimator of variance σ², as we know that we should divide by n − 1 rather than n. However, it is a consistent estimator, since when n → ∞, there is no difference between dividing by n − 1 or n. Incidentally, by dividing by n we lose unbiasedness but we retain consistency while reducing variance.