Factor analysis is another interdependence technique, which shares some theoretical background with PCA, as we show in Section 17.3. Factor analysis can be used for data reduction, too, but it should not be confused with PCA, as in factor analysis we are looking for hidden factors that may explain common sources of variance between variables. Formally, we aim at finding a model such as
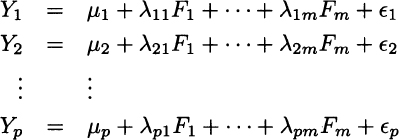
where the variables Yi are what we observe, Fj are common underlying factors, 
are individual sources of variability, and m is significantly smaller than p. This may look like a set of regression models, but the main difference is that factors are not directly observable. We are trying to uncover hidden factors, which have to be interpreted. Even though the above equations suggest a dependence structure between the observations and the underlying factors, there is no dependence structure among the observations themselves; hence, factor analysis is considered an interdependence method for dealing with metric data. It is natural to use factor analysis for exploratory purposes, but it can also be used for confirmatory purposes.
Leave a Reply