A demonstration of the Uncertainty Principle is simple to conduct using a laser pointer and an adjustable slit consisting of two razor blades. The idea is that the photons emitted by the laser travel without diverging. As shown in Figure 104, the photons exiting the laser can be assumed to have momentum only along the x axis (so py = 0). However, the exact position of a photon in the beam is unknown.
Figure 104 Heisenberg’s Uncertainty Principle applied to a particle passing through a slit.
The position of the photons can be better localized by passing the beam through a slit of width s. This essentially turns the slit into a position-measuring apparatus. However, intercepting the photon beam with a slit will introduce some momentum in the y direction. The more you localize the position of the photon by closing the slit, the more you will become uncertain about the momentum that the photon will have after passing through the slit. This becomes noticeable as a broadening of the diffraction pattern in the y direction, which means that by measuring the position of the photons you have given them some momentum along the y axis that was not there before they encountered the slit.
Given de Broglie’s particle–wave relationships, the same exact experiment could be performed with particles that have mass, so let’s not restrict the analysis to photons. We’ll go slowly so that the math is clear:
For a particle passing through a slit of width s, we know that the particle must be within the slit, so our uncertainty in position along the y axis is:
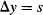
Before passing through the slit, the particles only have momentum along the x axis (so py = 0). However, after passing through the slit, the particles will have some momentum component in the y axis (p’y ≥ 0).
A diffraction pattern is obtained when we pass light through a single slit. The first minimum in the pattern happens at an angle θ that obeys:
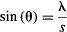
so
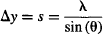
De Broglie tells us the same would happen for any particle, so the particle’s uncertainty (one standard deviation) is well approximated by:
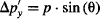
The particle’s momentum and de Broglie wavelength of a particle are related by:
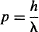
so,
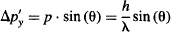
Multiply the uncertainty in momentum Δp’y by the uncertainty in position Δy:
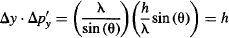
Which was Heisenberg’s original estimate for the uncertainty trade-off between position and momentum of a particle!
To conduct this experiment, we made an inexpensive variable slit using a low-cost digital caliper and two single-edge razor blades. We carefully taped each blade to a jaw of the caliper, as shown in Figure 105a, using double-sided tape. We then aimed a laser pointer at the gap between the blades and observed the single-slit diffraction pattern on a distant screen. The pattern scanner that we built (Figure 5) also works well for measuring single-slit diffraction patterns.
Figure 105 Demonstrating Heisenberg’s Uncertainty Principle with photons is easy to do with a laser pointer and a single slit. (a) We constructed an inexpensive variable-width slit from a low-cost digital caliper and two single-edge razor blades. (b) Measurements of the distance to the first minimum in the diffraction pattern should be taken for a number of slit widths and laser wavelengths.
In our experiment, the angle θ is estimated by measuring the position of the first minimum d:

where d is the measured fringe separation and r is the distance between the slit and the screen.
Which lets us determine the uncertainty in momentum through:
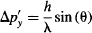
Since Δy = s, Heisenberg’s Uncertainty Principle is confirmed if:
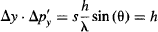
or dividing by h, if:
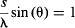
Go ahead—set up this simple experiment and measure θ for a number of slit widths (e.g., 0.05, 0.1, and 0.2 mm) and laser wavelengths. Using our measurements, we came up with an average value for s/λ sin (θ) of 1.05, which confirms Heisenberg’s Uncertainty Principle within our experimental limits of error.
Another interesting way of conducting this experiment is by using the microwave optics stand we constructed (Figure 17), placing a single slit in the slide holder, and determining the angles where the minima appear for the system’s 2.85-cm-wavelength photons (Figure 106). As the goniometer arms are moved, you should find a first dip in the signal at sin (θ) = λ/s. Good slit widths for this experiment are 7 cm and 13 cm.
Figure 106 An interesting way of confirming Heisenberg’s Uncertainty Principle is to measure the single-slit diffraction of a microwave beam using the Gunnplexer. (a) The angle is measured directly using the goniometer stand. (b) With this geometry, the first dip in the diffraction pattern should appear at s(sin θ) = λ.
Experiments using the same basic concept have been used by Zeilinger’s team in Austria to prove Heisenberg’s Uncertainty Principle with objects as large as fullerene molecules containing 70 carbon atoms.31
Leave a Reply