From equation:
Example 1.18: A heat engine having an efficiency of 35% is used to run a refrigerator of COP of 4, what is the heat input into the each MJ removed from the cold body by the refrigerator? If this system is used as a heat pump (Figure 1.16), how many MJ of heat would be available for heating for each MJ of heat input to the engine?
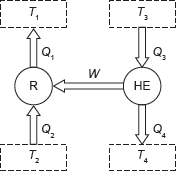
Figure 1.16 Heat Reservoir and Sink
Solution:
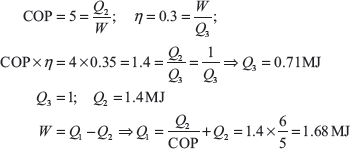
Example 1.19: A heat pump working on a Carnot cycle takes in heat from a reservoir at 8°C and delivers heat to the reservoir at 50°C. The heat pump is driven by a reversible heat engine taking heat from a reservoir at 850°C and rejecting heat to reservoir at 50°C (Figure 1.17). The reversible heat engine also drives a machine of input required of 25 kW. If the heat pump extracts 15 kJ/sec from the 8°C reservoir, determine (a) the rate of heat supply from the 850°C source, and (b) the rate of heat rejection to 50°C sink.
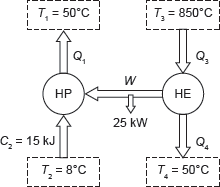
Figure 1.17 Heat Pump and Heat Engine
Solution:
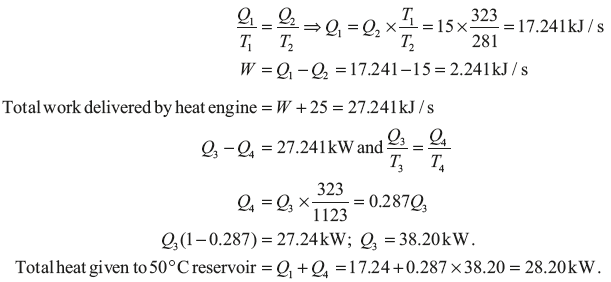
Example 1.20: A reversible heat engine as shown in Figure 1.18 during a cycle of operation draws 5 MJ from the 400 K reservoir and does 840 kJ work. Find the amount and direction of heat interaction with other reservoirs.
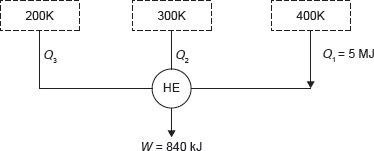
Figure 1.18 Reversible Heat Engine
Solution:


Solving Eqs (1.1) and (1.2), we get
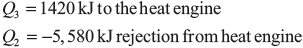
Example 1.21: Two blocks of metal each of mass M and specific heat C, initially at absolute temperature T1 and T2, respectively, brought to the same final temperature Tf by means of reversible process. Derive an expression for the amount of work obtained during the process in terms of M, C, T1 and T2.
Solution:
Let T1 > T2 and final temperature be Tf.
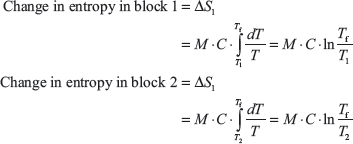
For reversible process, total entropy = 0
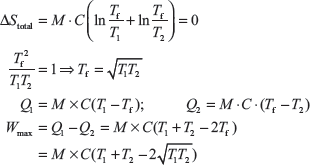
Example 1.22: An insulated tank of 1 m3 volume contains air at 0.1 MPa and 300 K. The tank is connected to high pressure line in which air at 1 MPa and 600 K flows. The tank is quickly filled with air by opening the valve between the tank and high pressure line. If the final pressure of air in tank is 1 MPa (Figure 1.19), determine the mass of air which enters the tank and the entropy change associated with filling process. Take universal gas constant ![]() = 8.314 kJ/kg mole K.
= 8.314 kJ/kg mole K.
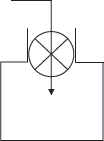
Figure 1.19 Insulated Tank
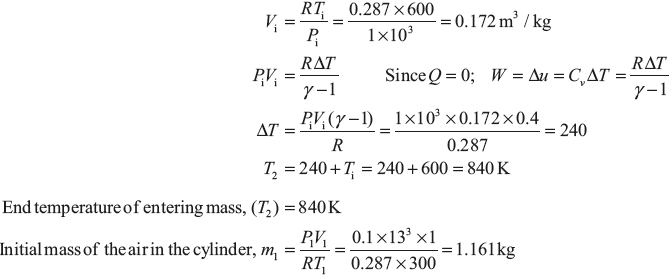
Let final mass of air inside the cylinder = m2
Final temperature of air inside the cylinder = T
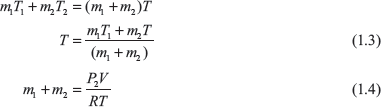
From Eqs (1.3) and (1.4)
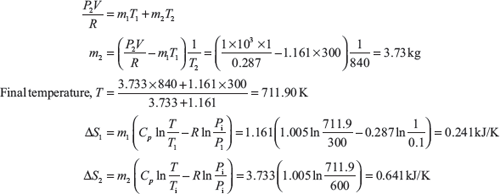
Entropy change associated with the process = ΔS1 + ΔS2 = 0.88261 kJ/K
Example 1.23: Ten kilograms of water at 0°C is brought into contact of a heat reservoir at 100°C, where water temperature becomes 100°C. Find the entropy change of water, reservoir and universe.
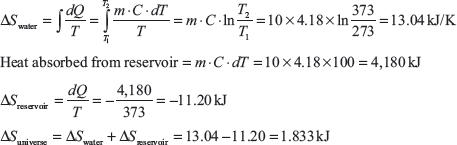
Example 1.24: Calculate the entropy change when 5 kg of water at 20°C is mixed with 5 kg of water at 100°C. The specific heat of water is 4.18 kJ/kg.
Solution:
Let Tf is final temperature
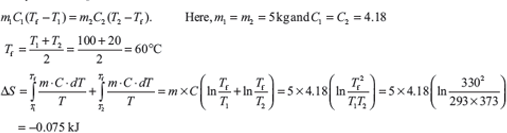


Leave a Reply