Because we know exactly what the electric field looks like surrounding a positively charged proton, it is easy to specify the potential energy we need to put into the three-dimensional version of the Schroedinger equation. But now it turns out to be more useful to use a potential energy scale where zero is the maximum, so that all potential energies are negative.
ATOM TRAP
Don’t be confused by our decision to fix our potential energy such that the electron’s potential energy is negative. This doesn’t mean we’re describing some bizarre universe where pigs fly backward and bombs neatly assembly themselves upon detonation. We can do this because, at the end of the day, all that really matters are differences in potential energy at different positions, and differences are differences regardless of whether potential energy is defined as being positive or negative.
Maxwell’s equations can be manipulated to show that the potential energy of an electron relative to the proton is inversely proportional to the distance between the two. This means that at a large distance from the proton, the potential energy approaches zero as you would expect. On the other hand, as the electron nears the proton, the potential energy will drop significantly. If you were to plot the potential energy as a function of the electron’s distance from the proton, you’d see a potential well that gets extremely deep as this distance goes to zero. It actually drops off to negative infinity, but because there is vanishingly small volume at such small distances, and because the proton itself is extremely small, this turns out not to bother us at all.
A semester or two of university-level calculus is about all we need to solve the Schroedinger equation when this potential energy function is included. The result is a set of valid solutions that, of course, are three-dimensional wave functions. But despite this additional richness, they share some key features with the wave functions we have just been talking about.
QUANTUM LEAP
When Schroedinger locked himself in his Alpine chateau over Christmas of 1925, hunkered over de Broglie’s thesis and determined to find a wave-based foundation of quantum mechanics, the problem he attacked was the hydrogen atom. In this sense, he came up with his famous equation by studying the very problem we’re discussing here.
The first is that the solutions are, in a very real sense, standing waves. The reason for this is basically the same as it was in our one-dimensional examples: the values of the wave function and its slope have to vary smoothly in space and match everywhere. But now the matching doesn’t have to happen at some artificial boundary, it has to happen because of the structure of three-dimensional space itself. We saw this already in the two-dimensional, standing-wave Bohr orbits shown in the figure.
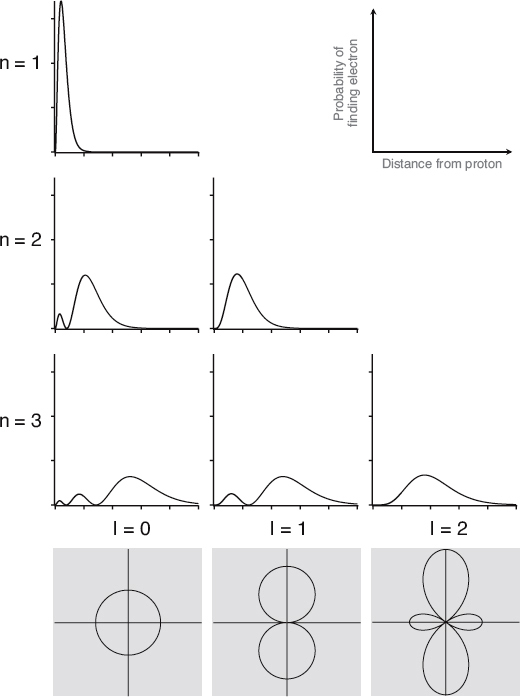
This figure depicts the spatial properties of several hydrogen atom wave functions. The panels at the top show the probability of finding an electron as you move away from the proton for various combinations of n and l. The “humps” between nodes are commonly referred to as electron clouds. The three shaded panels at the bottom show the approximate “shape” of the wave functions for the three different l values. As l increases, so does the complexity of the wave functions.
Like the one-dimensional standing waves we saw earlier in this three-dimensional standing wave patterns depicted in the figure here also have nodes (or locations where the wave function is zero). The difference now is that a node is not just a single point in one dimension; it can be a curvy surface in three-dimensions. Since the wave function has zero amplitude at the nodes, there must be regions between nodes where the wave function has large amplitude, and therefore where it is more likely to find the electron. Thus the nodes are like boundaries between fuzzy clouds of probable electron locations, which are often referred to as “electron clouds.” We show you a few of these in the figure here. Of course, we can also think about the different wave function solutions as different probability distributions for the location of the electron.
Leave a Reply