Technology evaluation encompasses not only technical feasibility of a particular technology but also the economics of its implementation. While there are many measures of economic merit, two measures – investment and net present value (NPV) – provide a complete set of information on which to base an informed, economic decision. “Investment” refers to the money that must be spent initially to design and build the new facilities. NPV is the after‐tax worth in today’s dollars of all the future cash that an alternative will either consume or generate; it includes the effects of new investment, working capital, operating costs, revenues, and income taxes. NPV is the most popular singular measure of the economic merit of an alternative, and many spreadsheet programs can easily calculate it.
To evaluate alternative pollution control devices, the analyst must be able to compare them in a meaningful manner. Since different controls have different expected useful lives and will result in different CFs, the first step is to use the principle of the time value of money to normalize the returns of the alternatives being compared. The process through which future CFs are translated into current dollars is called present value (PV) analysis. When the CFs involve income and expenses, it is also commonly referred to as NPV analysis. In either case, the calculation is the same: adjust the value of future money to values based on the same (generally year zero of the project), employing an appropriate interest (discount) rate and then add them together. The decision rule for NPV analysis is that projects with negative NPVs should not be undertaken; and for projects with positive NPVs, the larger the NPV, the more attractive the project. Derivation of a CF’s NPV involves the following steps:
- Identification of alternatives – for example, the choice between a fabric filter baghouse and an electrostatic precipitator for removing particulate matter from a flue‐gas stream.
- Determination of costs and CFs over the life of each alternative.
The relationship of the future value of money to the PV of a sum of money compounded annually at an interest rate, i, for a total of n years is shown by the following equation:
where
- FV = future value
- PV = present value
- i = annual earnings rate
- n = years in the future
This equation is used to determine how many future dollars will be realized by investing present dollars at the interest rate i for n years. For example, $100 invested today at 5% for 12 years will yield the following return:
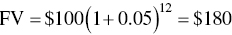
Similarly, inflation at 5% per year makes $100 worth of merchandise today cost $180 in 12 years. Discounting is the opposite of compounding: the PV of a sum of money to be spent or received in the future is reduced according to
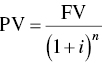
where i is now referred to as the discount rate. Thus, if the discount rate is 5% per year, we calculate the PV of $100 to be spent 12 years as follows:
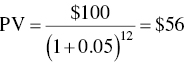
Since the PV of money to be spent in the future declines with increasing interest rate and number of years into the future, the importance of accounting for the time at which money is spent or received is evident.
Leave a Reply