Diffusion of contaminants in workplace air results in the net movement of the contaminants from regions of higher concentration to regions of lower concentration. The spread of the contaminant is aided by the advective mass transfer driven by the ventilation system. The combination of these influences results in movement of contaminants away from their source into the surrounding room.
The mass‐balance model presumes a uniform concentration of the chemical contaminant in the work area. Dispersion models have a notable advantage; they describe the variation of contaminant concentration with distance from the source. The concentration gradient is described by the following equation when advection occurs in the x‐direction only and dispersion occurs equally in all directions:
(4.14)
where
- u is the air velocity in the x‐direction (length/time)
- C is the concentration of airborne contaminant (mass/length3)
- D is the diffusion coefficient (length2/time)
- x is the distance downwind from the source (length)
- r is the distance from the source to the sampling point (length)
This equation has been solved for concentrations resulting from emissions into an infinite space:
where G is the contaminant emission rate from the source (mass/time).
The diffusion coefficient (D) can be derived from measurements at the sampling site or estimated from values available in the literature. Measurements of the diffusion coefficient in indoor industrial environments have ranged from 0.05 to 11.5 m2/min, with 0.2 m2/min being a typical value.
EXAMPLE 4.12
Freon is emitted from an open‐top vapor degreaser at a rate of 0.74 g/min. Estimate the concentration in the air inhaled by a worker 3 m downwind from the degreaser if the air velocity is 0.79 m/min.
SOLUTION
Since the worker is downwind of the degreaser, x = r in the diffusion convection equation (Eq. 4.15) and
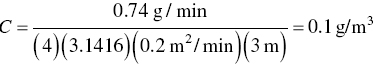
Molecular diffusion theory strictly applies to vapors and gases; however, PM with aerodynamic diameters less than 10 μm are distributed in workplace air in a similar manner. Using the dispersion models to describe the distribution of dusts and fumes is reasonable for small particles.
Gaussian Dispersion Model
The Gaussian dispersion model is most often used to characterize the dilution of toxic air pollutants with distance from the source. The model provides reasonable agreement with the experimental data and is, in its simplest form, calculations with. The mean concentration, C, resulting from emission at a continuous point source of strength Q at a height H above the totally reflecting Earth along the plume centerline is given by
where
- C is the concentration of toxic air pollutant (μg/m3)
- Q is the source release rate (μg/s)
- U is the mean wind speed at the stack height (m/s)
- H is the effective height of release above the Earth (m)
- y is the distance in a direction transverse to the wind (m)
- z is the height at which the observation is made (m)
- σ y and σ z are the standard deviations of the concentrations of plume transverse to the wind and perpendicular to the Earth, respectively (m).
Published values of σ y and σ z are based on laboratory and field measurements of velocity fluctuations under a variety of atmospheric conditions. Atmospheric stability is used to represent the amount of mixing in the atmosphere and is generally classified as stable, neutral, or unstable. A stable atmosphere is characterized by temperatures that increase with distance from the surface of the Earth and reduced vertical mixing; nighttime atmospheric conditions are generally represented as stable. More vigorous atmospheric mixing is expected as the Sun warms the surface of the Earth and the warmer, less dense air accumulates near the Earth’s surface; eventually, gravity will displace the warm air with cooler air from above. Daytime atmospheric conditions are typically represented as either neutral or unstable.
The product of the standard deviations has been represented by an equation of the form
(4.17)
where
- a and b are constants (nondimensional)
- x is the distance downwind from the source (length)
Kumar (1998, 1999) performed regression analysis to develop expressions for the constants, a and b, for urban and rural settings and neutral and stable atmospheric conditions. Urban settings are appropriate when there are many obstacles in the immediate area of the release; obstacles include buildings and trees. Rural settings are appropriate when there are no buildings in the immediate area of the release and the terrain is generally flat and unobstructed. Table 4.10 lists the results of the regression when the distance from the source is in meters.
EXAMPLE 4.13
Hydrogen sulfide is released from a low‐level vent in a rural area at a rate of 0.025 kg/s. Calculate the concentration at the plant boundary located 300 m downwind from the vent during daytime conditions when the wind speed is 4 m/s and at night when the wind speed is 2.5 m/s. (a) If the concentration of concern for hydrogen sulfide is 42 mg/m3, will this concentration be exceeded at the plant boundary? (b) Estimate the exposure to hydrogen sulfide of a person living 300 m downwind from the facility described during (i) daytime and (ii) nighttime if the individual at rest breathes 0.9 m3/h of the ambient air.
SOLUTION
- Equation (4.16) can be used to calculate the concentration at ground‐level by setting the height above the Earth equal to zero. The appropriate correlations for the dispersion coefficients are given by items (a) and (c) in Table 4.10 for daytime and nighttime conditions, respectively. For daytime conditions,
For nighttime conditions,
The concentration of hydrogen sulfide is below the concentration of concern under daytime conditions but exceeds the concentration of concern at night when atmospheric mixing is less. - For daytime condition, (7.17 mg/m3)(0.9 m3/h) = 6.45 mg/hFor nighttime conditions, (50.2 mg/m3)(0.9 m3/h) = 45.2 mg/h
Leave a Reply