Disappointment and regret in decision making

When making decisions under risk and uncertainty in our lives, we rarely set up a utility function to formalize the problem we are facing. We come up with a solution but, unfortunately, sometimes we must admit that we were wrong. Indeed, disappointment and regret are emotions that we have all experienced. A discussion of disappointment and regret may seem more akin to psychology than business decision making. However, they can provide an explanation for some typical paradoxes of decision-making models based on the assumption of full rationality.

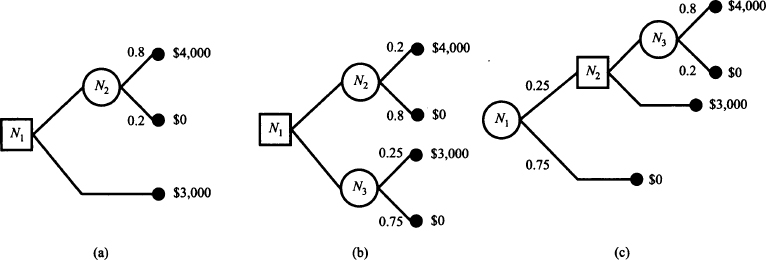
Fig. 13.12 An example illustrating the effect of disappointment.

Example 13.12 Consider the decision trees depicted in Fig. 13.12.²⁷ In Fig. 13.12(a), the decision maker must choose between a lottery, with expected payoff

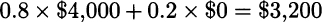
and $3,000 for sure. Most people prefer the certain payoff, which is consistent with the idea of risk aversion. In Fig. 13.12(b) we are comparing two lotteries, whose expected payoffs are

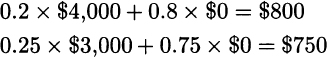
respectively. In this case, empirical research shows that most people prefer the first lottery.²⁸ Arguably the increase in win probability is not enough to compensate for the reduction in the payoff. Now consider Fig. 13.12(c). Here, the root of the decision tree is a chance node, rather than a decision node. This basically means that a biased coin is flipped first; with probability 0.75 the game stops immediately; with probability 0.25, the decision maker is faced with the same situation depicted in decision tree (a). If we see things this way, common sense suggests that the decision should be the same as in case (a): Go for the sure payoff.²⁹ Furthermore, the decision maker should not object if requested to make her choice before the flip of the coin, thus defining a strategy. However, if we carry out a few calculations, it is easy to see that tree (a) is nothing but tree (b) in disguise:

• If the strategy selects the lower branch for the decision node in (c), there is an a priori probability 0.25 × 1 = 0.25 of winning $3,000.
• If the strategy selects the upper branch for the decision node in (c), there is an a priori probability 0.25 × 0.8 = 0.2 of winning $4,000.

Now we see a contradiction with the standard choice in case (b). A bit of reflection suggests that a rational decision maker should either select the upper or the lower branches in all of the three cases. But this is at odds with what is empirically observed. Hence, we must be missing something.

A possible explanation of the weird finding of Example 13.12 is based on disappointment and regret. Imagine taking your chances in the case of Fig. 13.12(a). If you go for the lottery and you lose, you will certainly regret your decision, since you have wasted $3,000 for sure. Then, rather than feeling so sorry, it might be better to choose the safer option. In Fig. 13.12(b), the probability of winning is low for both lotteries. You are likely lose in both cases: Whatever you choose, you will not feel too sorry. Hence, you may just go for the lottery with higher payoff in case of win, which is also the lottery with the higher expected payoff. Now consider the situation of Fig. 13.12(c). If, after the first flip, you are out of the game, so be it. You will be sorry, but there is nothing to regret, as this outcome did not depend on your choice. But in the lucky case you enter the lottery at the second stage, you will certainly be disappointed if you end up losing $4,000 rather than grabbing $3,000 for sure. Hence, chances are that in this case you will go for the safer option, even though this contradicts the choice in case (b). A formal framework for modeling disappointment has been proposed in Ref. [3], where expected economic utility is integrated with a psychological view of decision maker’s behavior. In fact, the paradigm of expected utility is at odds with quite some share of observed behavior, and this has suggested alternative frameworks.

So far, we have been a bit ambiguous when speaking about disappointment and regret. They are certainly related, but different emotions.³⁰ To see the difference, consider the following experiments:³¹

• You spin a simple fortune wheel, where you may just win or loose. There is a high probability that you will win the prize, but unfortunately the outcome is unsatisfactory. You will be disappointed, but no decision was involved: You are comparing the actual outcome with a better one that might have resulted.
• You must spin one of two fortune wheels, say, A and B. Suppose that you select wheel A. Then both wheels are spun, and you lose. To add insult to injury, you are shown that the result from wheel B is “win.” Then, you will experience regret, as a better outcome would have resulted, had you made a different choice.

It may seem that the role of emotions in decision making is disconnected from business management. However, there are indeed cases in which regret is what you should keep under control. Common features of such cases are:

• You are facing a nonrepetitive situation, where the law of large numbers does not apply; there is no point in making a decision that would prove the best one in the long run.
• You are evaluated ex post. Expectation is by definition ex ante, but imagine a situation in which your performance is assessed in comparison to what would have been the optimal decision, had you known the true value of uncertain parameters.

Min-max regret models have been proposed to address such situations. Consider the familiar cost function f(x, ω), where ω is a random event. To be specific, say that uncertainty may be represented by a set of scenarios ω_s ∈ S. If you knew that scenario ω_s is going to occur, you would solve the problem

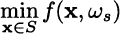
resulting in an optimal solution  and cost . Note that this is a rather simple problem that can be solved even for a rather large number of scenarios.³² Unfortunately, you have to solve the here-and-now problem, resulting in solution ; whatever model formulation you choose, some value of the objective function will result, but this is not what will affect your future career; the true ex post cost is what matters to your boss. The cost of the here-and-now decision, in scenario s, is . Unless you are very lucky, this will not be the optimal cost in scenario s, and you will experience a regret, formally defined as

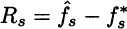
The idea is that, if scenario s occurs, you will discover that you had an extra cost R_s; the larger R_s, the larger the regret. However unfair this may sound, you could be just evaluated this way in real life: You might make a good and sensible solution, which turns out to be awkward if a bad scenario occurs. Then, a safer strategy could be to minimize maximum regret. By introducing an auxiliary variable ζ, this min–max model can be expressed as follows:

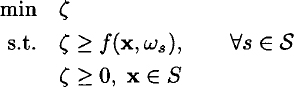
Several variations of the model, possibly including expected regret, may be formulated. If the original model was a linear programming problem, so will be the formulation based on regret.

Problems

13.1 Consider again the “fancy coin flipping” example of Section 1.2.3, i.e., the decision of producing a movie or not. Formalize the problem with a proper decision tree.

13.2 The Research and Development (R&D) division of your firm has developed a new product that could be immediately launched on the market. If so, the probability of success is 60%, in which case profit has a present value of €10 million (discounting all future cash flows). In case of flop, you will lose €2 million. You might also delay product launch by 6 months, in order to improve its design. This delay has advantages and disadvantages:

• Product improvement would cost €500,000, but it increases success probability to 90% (without changing hypothetical profits and losses); however, this applies only if no competitor takes advantage of your delay and enters the market, eroding your share (see the last bullet below).
• Delaying product launch has a financial impact, as cash flows are delayed; let us assume that the effect of delay is accounted for by a 5% discount rate for the 6 months. (Note: This is the rate applying to the 6 months, not to 1 year.)
• Delaying product launch has the effect of leaving room for the entry of competitors; we assume that the probability of this entry is 50% and its effect is not on success probability (which is still 90%), but on cash flows: Profit is halved, and loss is doubled, depending on product success or flop.

1. Assuming that you are risk-neutral, what would you do?
2. In practice all of the above probabilities are the result of educated guesswork. In particular, the entry probability is quite uncertain. Hence, you want to carry out a sensitivity analysis. What is the value of the entry probability (if it exists) that would make you change your mind with respect to the decision above?

13.3 You are the manager of a pension fund, and your fee depends on the return attained. You can play it safe and allocate wealth to a risk-free portfolio earning 4% per year. Alternatively, you can pursue an active portfolio management strategy, whose a return is normally distributed, with expected value 8% and standard deviation 10%. Your fee depends on the earned return according to the following tabulation:

Return (R)	Fee
R < 0%	$0
0% ≤ R < 3%	$50,000
3% ≤ R < 9%	$100,000
9% ≤ R	$200,000

• Which is your best strategy, if you are risk-neutral?
• What is the standard deviation of your fee, if you take the active strategy?

13.4 A decision maker with a quadratic utility function of the form (13.12) is offered the following lottery:

Probability	Payoff
0.20	$10,000
0.50	$50,000
0.30	$100,000

If the risk aversion coefficient is λ = 1/150,000:

• What is the certainty equivalent of the lottery?
• What is the risk premium?

13.5 You own a plant whose value is $100,000. In case of a fire, the value of your property might be significantly reduced or even destroyed, depending on how severe the accident is. Let us represent risk by the following scenarios:

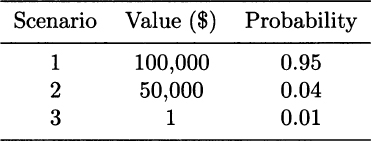
For each scenario, we have the value of your property and a probability. Clearly, in scenario 1 there is no fire and no loss. Assuming that your risk aversion is represented by a logarithmic utility function, what is the maximum insurance premium that you would be willing to pay? (Hint: The insurance would pay $0, $50,000, $99,999, respectively, in the three scenarios.)

13.6 An investor has an initial wealth W₀ that must be allocated between a risk-free asset, with certain return r_f, and a risky asset. We assume a simple binomial model of uncertainty, like we did in Section 3.1. The return of the risky asset will either be R_u or R_d, with probabilities p_u and p_d, respectively.

• Find the optimal allocation of wealth if the investor has an exponential utility function, like Eq. (13.11), with absolute risk aversion α.
• How does the value of the initial wealth influence the result?

13.7 You have invested $150,000 in stock shares of Doom and $200,000 in stock shares of Mishap. Assume that daily returns follow a multivariate normal distribution; daily volatilities for the two stock shares are 2% and 3%, respectively, and correlation is 0.8. Find the one-day VaR at 99% confidence level.

13.8 We know that VaR, in general, is not a subadditive risk measure. Consider a portfolio of two assets, with jointly normal returns.

• Show that, in this specific case, VaR is a subadditive risk measure.
• Is standard deviation a subadditive measure in the case above? What can we say in general?

13.9 Consider the plant location model of Section 12.4.5 [see Eqs. (12.54–12.55)]. Adapt the model to cope with uncertain demand scenarios, building a two-stage stochastic linear programming model with recourse.

13.10 Consider a point-to-point transportation network consisting of M nodes. By “point-to-point” we mean that, given transportation requirements between all pair of nodes, there is a direct transportation link from each origin to each destination, without transshipment through intermediate nodes (this should be understood as a simplification of the real-life problem). Each node, in general, is both a source and a destination for many such requirements. Transportation requires containers of given volume capacity, measured in the same units as transportation requirements. At present, we know how many empty containers are present at each node in the network. Before transportation needs arise, we should consider repositioning containers, so that we will be in a better position to meet all requirements. Repositioning is carried out now, and transportation occurs in the next period. We know the repositioning cost for each container, for each pair of nodes in the network (say that they essentially depend on traveled distance). What we do not know are the future transportation requirements, but we are able to generate a set of plausible scenarios. Each scenario is essentially a matrix describing the transportation requirement for each pair of nodes (the diagonal elements are zero), associated with a probability. If, when requirements are revealed, we do not have enough containers to satisfy them at a node, we have to rent containers, which implies a rather high fixed cost per container. For the sake of simplicity, let us assume that such cost does not depend on nodes, nor traveled distances. On the one hand, we would not like to move too many containers; on the other one, we do not want to spend too much money to rent containers if spikes in transportation demand occur at some nodes. Build a two-stage stochastic programming model to minimize the total expected cost.