Figure 13.6 shows the arrangement of differential wheel and axle. It is used to lift the heavier loads. In this lifting machine, the axle is made up of two cylindrical axles B and C of different diameters d1 and d2, respectively. Wheel A has larger diameter, D. The wheel A and axles B and C are keyed to the same shaft. The string is wound on the axle B and C in such a way that if the shaft rotates, the string unwinds on the axle C and winds at the same time on axle B, thereby lifting the load W attached to the snatch block. String on the wheel A and string on the axle C must wound in the same direction. During the unwinding from the wheel A, the other string should unwind on axle C and wind on axle B.
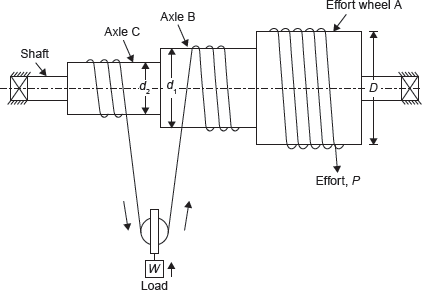
Figure 13.6 Differential Wheel and Axle
Let P = Effort applied on wheel A
W = Load lifted by axle
D = Diameter of effort wheel A
d1 = Diameter of load axle B
d2 = Diameter of load axle C
Since the wheel A, axles B and C are keyed to the same shaft thus, the number of revolution of the wheel and axles per unit time will be same.
For one revolution of wheel and axle,
Distance moved by the effort, P = πD
Distance moved by a point on axle, B = πd1
Distance moved by a point on axle, C = πd2
The distance through which the load W is lifted = ![]()
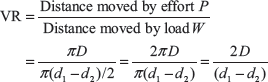

Example 13.5: In a differential wheel and axle, the diameter of wheel is 12 cm and that of axles are 6 and 4 cm. If the efficiency of the machine is 75% find the effort required to lift a load of 250 N. Calculate the number of revolutions made by the machine in lifting the load by a distance of 22 cm.
Solution:
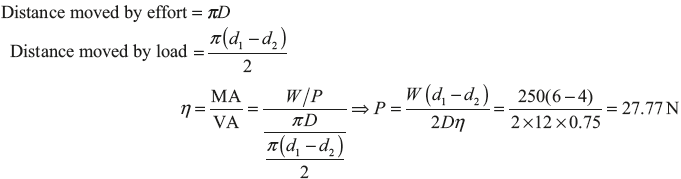
∴ Distance moved by the load is ![]() in one revolution.
in one revolution.
∴ Distance moved by the load is 22 cm in ![]() revolution.
revolution.
Leave a Reply