Development of the Radial Diffusivity Equation

The radial diffusivity equation, which is the general differential equation used to model time-dependent flow systems, is now developed. Consider the volume element shown in Fig. 8.12. The element has a thickness Δr and is located r distance from the center of the well. Mass is allowed to flow into and out of the volume element during a period Δt. The volume element is in a reservoir of constant thickness and constant properties. Flow is allowed in only the radial direction. The following nomenclature, which is the same nomenclature defined previously, is used:

q = volume flow rate, STB/day for incompressible and slightly compressible fluids and SCF/day for compressible fluids

ρ = density of flowing fluid at reservoir conditions, lb/ft³

r = distance from wellbore, ft

h = formation thickness, ft

ν = velocity of flowing fluid, bbl/day-ft²

t = hours

φ = porosity, fraction

k = permeability, md

μ = flowing fluid viscosity, cp

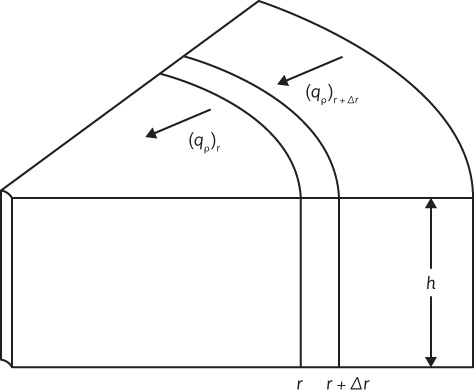
Figure 8.12 Volume element used in the development of the radial differential equation.

With these assumptions and definitions, a mass balance can be written around the volume element over the time interval Δt. In word form, the mass balance is written as

Mass entering volume element during interval Δt – Mass leaving volume element during interval Δt = Change of mass in volume element during interval Δt

The mass entering the volume element during Δt is given by

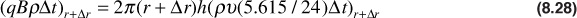
The mass leaving the volume element during Δt is given by

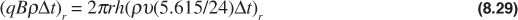
The change of mass in the element during the interval Δt is given by

Combining Eqs. (8.28), (8.29), and (8.30), as suggested by the word “equation” written above,

2π(r+r)h(ρυ(5.615/24)Δt)_r+Δr –2πrh(ρυ(5.615/24)Δt)_r = 2πrΔrh[(φρ)_{t + Δt} – (φρ)_t]

If both sides of this equation are divided by 2πrΔrhΔt and the limit is taken in each term as Δr and Δt approach zero, the following is obtained:

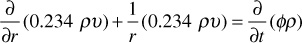
or

Equation (8.31) is the continuity equation and is valid for any flow system of radial geometry. To obtain the radial differential equation that will be the basis for time-dependent models, pressure must be introduced and φ eliminated from the partial derivative term on the right-hand side of Eq. (8.31). To do this, Darcy’s equation must be introduced to relate the fluid flow rate to reservoir pressure:

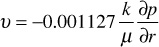
Realizing that the minus sign can be dropped from Darcy’s equation because of the sign convention for fluid flow in porous media and substituting Darcy’s equation into Eq. (8.31),

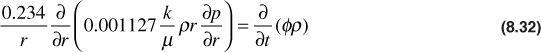
The porosity from the partial derivative term on the right-hand side is eliminated by expanding the right-hand side and taking the indicated derivatives:

It can be shown that porosity is related to the formation compressibility by the following:

Applying the chain rule of differentiation to ∂φ/∂t,

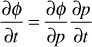
Substituting Eq. (8.34) into this equation,

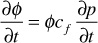
Finally, substituting this equation into Eq. (8.33) and the result into Eq. (8.29),

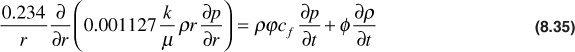
Equation (8.35) is the general partial differential equation used to describe the flow of any fluid flowing in a radial direction in porous media. In addition to the initial assumptions, Darcy’s equation has been added, which implies that the flow is laminar. Otherwise, the equation is not restricted to any type of fluid or any particular time region.