Each photon in an entangled-photon pair is just a photon, and like any other photon, it can be detected using the type of methods that we used (Figure 33) to detect individual photons.
However, recall that the quantum efficiency of the PMT probe that we built (Figure 30) was quite low, even at high photon energies (a maximum of 25% at 400 nm, as shown in Figure 33b). This becomes a major problem when working with entangled photons, since we want to count coincident detections when each photon is challenged in a different way in order to test their entanglement. Worse, the PMT we used is completely unresponsive to the IR photons produced by parametric down-conversion in BBO with a 405-nm pump.
Detecting individual photons at 810 nm with reasonable quantum efficiency is possible, but requires specialized detectors that are very expensive. One option is to use a low-noise PMT that is sensitive to these wavelengths—and there aren’t many on the market. A possible candidate is Hamamatsu’s model H7421-50 photon-counting module with a quantum efficiency of 12% at 810 nm. This module uses a metal-package PMT with a thermoelectric cooler that is necessary to reduce thermal noise generated from the photocathode. It is obviously quite a sophisticated piece of equipment, and retails at around $4,000 each (we need a minimum of two units to perform experiments with entangled-photon pairs).
A better alternative is to use a probe based on a semiconductor photodetector known as a single-photon avalanche diode (SPAD), which can reach quantum efficiencies as high as 80% at 810 nm. These detectors work somewhat like Geiger tubes (Figure 56); as you may remember the gas mixture and operating voltage in a GM tube are chosen so that a single ionizing event caused by a gamma photon leads to an avalanche of ionization to produce a more easily detectable pulse. However, unlike in a GM tube, the avalanche in a SPAD (which doesn’t happen in a gas, but in a solid semiconductor diode) is not extinguished (quenched, in the parlance of physicists) by itself, so the circuit must be designed to interrupt the current through the SPAD, readying it to detect a new photon.
As shown in Figure 143, a SPAD-based single photon–counting module (SPCM) commonly comprises a discrete SPAD packaged in a hermetic enclosure together with a thermoelectric cooler (TEC). The cooler is a module based on the Peltier Effect, which pumps heat away from the SPAD to an external heat sink when powered. The TEC is very similar to the modules used in portable beverage coolers. It is a simple device formed by a semiconductor sandwich that pumps heat in one direction when a DC current is applied between its terminal electrodes. A T/C sensor is commonly attached to the TEC, allowing an external circuit to control the current flowing through the TEC to maintain the SPAD’s temperature at an optimal level.
Figure 143 Modern SPCMs use SPADs as detectors. The SPAD is biased at a high voltage, which allows a single photon to cause an avalanche breakdown similar to what happens in a GM tube. However, the avalanche in the SPAD is not extinguished by itself, so a quenching circuit must be used to interrupt the current through the SPAD, readying it to detect a new photon. A thermoelectric cooler is used to keep the SPAD at a low temperature (typically 0°C to -20°C) to reduce false counts (“dark counts”).
The SPAD is biased through a resistor to a relatively high voltage that depends on the specific device. Typical operating voltages are in the range of 50–250 V. A photon entering the SPAD triggers an avalanche current within the SPAD that is easy to detect through an AC-coupled pulse amplifier. The avalanche current must be interrupted and the bias voltage restored before the SPAD is ready to detect a new photon. The quenching circuit to interrupt the avalanche current may be implemented through simple passive biasing, using correctly matched resistors, or through an active mechanism that forcibly turns off and then restores the bias to the diode when a photon is detected. In general, active circuits are much more complex, but allow the SPAD to detect consecutive photons at rates that passive quenching would miss. Passive quenching is now more commonly being applied in newer designs, and some of the newer devices even integrate a quenching mechanism embedded within the SPAD, providing effective feedback for stabilization and quenching of the avalanche process without any external support circuitry.
There are very few SPAD manufacturers. The most notable are PerkinElmer (as part of their Excelitas Technologies division), and Laser Components. However, applications for SPADs are expanding, particularly in biomedical applications such as DNA sequencing, so their availability and pricing may eventually bring them within range of a larger number of physics experimenters. Table 9 shows some of the currently available commercial SPADs that can be used to detect entangled photons at wavelengths close to 810 nm.
TABLE 9 Characteristics of Some Commercial TEC-Cooled Single-Photon Avalanche Photodiodes Suitable for Experiments with Entangled Photons at an Approximate Wavelength of 810 nm
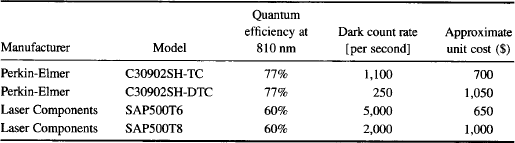
Figure 144 shows the schematic diagram for a passively quenched SPCM based on a Perkin-Elmer C30902S-DTC SPAD. Besides our design, you may also want to take a look at the high-performance, relatively low-cost design for an actively quenched SPCM based on this same SPAD that was undertaken as a senior design project at the University of Illinois. Their report, including complete schematics, is available online.65 Please note that gaining sufficient experience to build a high-performance SPCM is difficult when working with SPADs that cost around $1,000 apiece, so you should try to build this device only if you are very familiar with the construction of low-noise electronic systems that incorporate high-speed logic. Acquiring ready-made SPCMs may sometimes be a better alternative (e.g., Perkin-Elmer SPCM-AQRH at around $2,600 each for the 250 dark counts/s version, or the 1,100 dark counts/s version for $2,250).
Figure 144 Two TEC-cooled SPADs are used to build two SPCMs. The SPCM outputs are processed by two 74ACT74 dual D-type positive edge-triggered flip-flops that perform pulse-stretching and coincidence-counting functions for Bell’s Inequality tests.
In the circuit of Figure 144, the SPAD is reverse-biased through a 200-kΩ resistor. This value is sufficiently large that an avalanche in the SPAD will be quenched by itself within less than a nanosecond. After quenching, the voltage across the SPAD recovers toward its original working bias voltage following an exponential increase with a time constant of around 400 ns. The SPAD does work while the bias is recovered, but at much lower photon-detection efficiency than at nominal bias voltage. The pulses produced by the SPAD are AC-coupled through C4 to a fast, constant-level discriminator built from a LT1719 fast comparator. The threshold level for the comparator is fixed at 22.5 mV. The LT1719 has an output that is compatible with TTL logic circuits. One of the dual D-type positive edge-triggered flip-flops inside a 74ACT74 IC shapes the comparator’s output into a 12-ns pulse every time a photon is detected.
The SPAD is cooled by a TEC module that is built into the SPAD’s package. The TEC controller is a dedicated circuit by ThermOptics that implements a feedback loop. The DN1225 operates from a single 5-V power source and is capable of supplying 2 A of current to a 2-Ω load with better than 90% efficiency. The device interfaces directly to the negative temperature coefficient resistor within the C30902S-DTC that senses the SPAD’s temperature. The temperature setpoint is selected via resistor R4 to cool the SPAD to -20°C. R8 sets the proportional gain to 500, and R10 sets the integrator time constant to 1 s. Finally, R11 sets the maximum voltage supplied to the TEC to 1 V. The DN1225’s proportional-integral control loop is capable of achieving a temperature stability of 0.01°C. The DN1225 is not always available, but ThermOptics’ DN1221 can also be used if the circuit is adapted to this module’s pinout.
The second SPCM is identical to the circuit we just described. The SPCM outputs are processed by a coincidence-counting circuit designed by Dehlinger and Mitchell from Reed College.45 Output pulses are 250-ns long, and should be fed to a three-channel counter. One possibility is using a PC-based digital timing/counting board (e.g., a PCI-6601 by National Instruments). Alternatively, you could feed the SPCMs’ outputs directly to the stand-alone coincidence counter shown in Figure 145 to test the CHSH version of Bell’s Inequality.
Figure 145 We use this two-channel photon and coincidence counter to monitor and tune our setup. (a) The SPCM outputs are processed by two 74ACT74 dual D-type positive edge-triggered flip-flops that perform pulse stretching and coincidence counting. The pulse width into each Veeder-Root A103-000 counter should be adjusted to 15 μs. The A103-008 allows counting to happen for a preset amount of time. (b) The circuit fits neatly within an 11-in. × 7-in. × 2-in. aluminum chassis. We used a sheet of breadboard material for the panel, because it makes it easy to cut rectangular holes for the Veeder-Root modules.
Leave a Reply