We have seen that a linear (affine) function f(x) = mx + q has a well-defined slope. Whatever value of the independent variable we consider, the slope of the function is always the same. If we are at point x and we move to point x + h, by any displacement h, the increment ratio14 is:

Fig. 2.16 A nonlinear function does not have constant increment ratios.
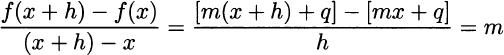
which is constant and does not depend either on x or h. The increment ratio, i.e., the rate of change in the function, is constant everywhere for a linear function and corresponds to the slope of the line. This does not apply to a nonlinear function like the exponential or the logarithm. The issue is illustrated in Fig. 2.16. Still, there are many reasons why we should be interested in investigating the “slope” of a nonlinear function:
- It may help in checking if the function is increasing or decreasing at some specific point x.
- It may help in evaluating the rate at which the function increases or decreases.
- It may help in finding a point at which the function is maximized or minimized.
This leads to the definition of a concept that is arguably the most important one in calculus: the derivative of a function.
Leave a Reply