The rules of previous section do not help us in finding derivatives of functions like the square root or, given the derivative of logarithm, in finding the derivative of the exponential. We need a rule to deal with the derivative of an inverse function.
THEOREM 2.9 (Derivative of an inverse function) Let x = g(y) be the inverse function of y = f(x). Then, subject to some technical conditions, the derivative of g is
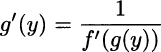
We will not insist on the conditions ensuring that the theorem holds. Of course, f must be invertible, which means that it must be monotonic on some interval; we also expect that some continuity is required in order to ensure differentiability, and the derivative f′ should not be zero. Leaving all of this aside, the best way to remember the result is by regarding it as
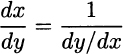
In practice, we should
- Find the derivative of f, f′(x)
- Evaluate it for x = g(y)
- Take the reciprocal of this value
Example 2.25 In Example 2.19 we saw that the derivative of f(x) = ln x is f′(x) = 1/x. On the basis of this finding, we may use Theorem 2.9 to find the derivative of its inverse, the exponential function g(y) = ey. Incidentally, the logarithm is continuous and increasing on its domain, so there is no problem in inverting it. The rule is applied as follows:
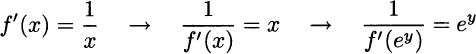
Thus, we see that the derivative of the exponential function, with base e, is the exponential itself.
Example 2.26 Now we are also able to find the derivative of the square root 
as the inverse of f(x) = x2. Following the inverse function drill, we have
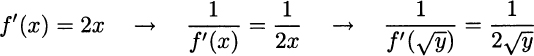
The behavior of the rate of increase for the square root function is similar to the natural logarithm.
One further thing that is worth noting is that we could have found the same result by formally applying the rule (xn)′ = nxn−1, for 
:
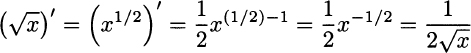
This formula can generalized as follows. Using the derivative of the inverse function, we might prove that the rule above can be applied to any power xm/n for integer numbers m and n; this means that the result applies to rational exponents; then, by limit arguments, it can be shown that it applies to any power xα, when α is a real number: (xα)′ = αxα−1.
Clearly, all of the rules that we have encountered can be applied together to deal with complicated functions, as Example 2.27 illustrates.
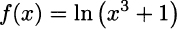
Using the derivative of natural logarithm and the derivative of composite functions, we get
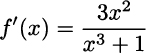
Needless to say, this makes sense for the domain of f(x), i.e., x3 + 1 > 0, or x > −1. By the same token, if
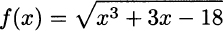
then
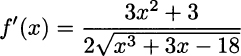
Leave a Reply