Given two functions g and h, we may build a new function by composition, namely, g o h. It would be nice to have a way of finding the derivative of the composite function by decomposing the task and exploiting knowledge about the derivatives of g and h.
THEOREM 2.8 (Chain rule) Given functions g and h, we obtain the derivative of their composition as
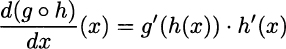
provided that all of the involved derivatives exist.
A good way to remember this rule is by rephrasing it in terms of increment ratios:

The idea is that we should take the derivative of function g(z) and evaluate it for z = h(x); then, this is multiplied by the derivative of h(x).
Example 2.23 As a first example, consider the exponential function f(x) = e4x. This is best viewed as the composition of functions g(z) = ez and h(x) = 4x. We know that
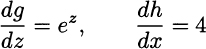
Hence, we apply the chain rule, where we set z = 4x in the first derivative:
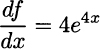
More generally, (eαx)′ = αeαx. This also applies to negative values of α. The case α = −1 can also be tackled by different route, considering the composition of g(z) = 1/z and h(x) = ex:
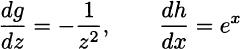
which yields
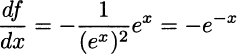
We invite the reader to check that
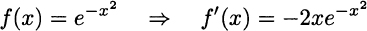
Example 2.24 Consider function f(x) = (x2 + 1)3. To find its derivative, we could use binomial expansion to transform it into a polynomial, but it is much easier to apply the chain rule:
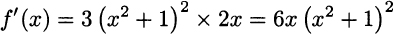
More generally, when we have a power of a function, like [f(x)]n, we obtain
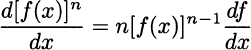
Leave a Reply