When an oil and gas reservoir is tapped with wells, oil and gas, and frequently some water, are produced, thereby reducing the reservoir pressure and causing the remaining oil and gas to expand to fill the space vacated by the fluids removed. When the oil- and gas-bearing strata are hydraulically connected with water-bearing strata (aquifers) with bulk volume much greater than that of the hydrocarbon zone, water encroaches into the reservoir as the pressure drops owing to production, as illustrated in Fig. 3.1. This water encroachment decreases the extent to which the remaining oil and gas expand and accordingly retards the decline in reservoir pressure. Inasmuch as the temperature in oil and gas reservoirs remains substantially constant during the course of production, the degree to which the remaining oil and gas expand depends on the pressure and the composition of the oil and gas. By taking bottom-hole samples of the reservoir fluids under pressure and measuring their relative volumes in the laboratory at reservoir temperature and under various pressures, it is possible to predict how these fluids behave in the reservoir as reservoir pressure declines.
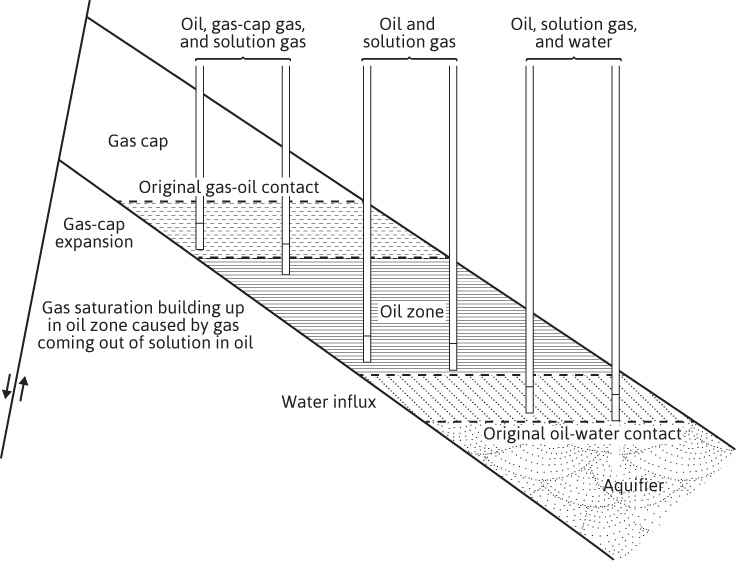
Figure 3.1 Cross section of a combination drive reservoir (after Woody and Moscrip, trans. AlME).5
It is shown that, although the connate water and formation compressibilities are quite small, they are, relative to the compressibility of reservoir fluids above their bubble points, significant, and they account for an appreciable fraction of the production above the bubble point. Table 3.1 gives a range of values for formation and fluid compressibilities from which it may be concluded that water and formation compressibilities are less significant in gas and gas cap reservoirs and in undersaturated reservoirs below the bubble point where there is appreciable gas saturation. Because of this and the complications they would introduce in already fairly complex equations, water and formation compressibilities are generally neglected, except in undersaturated reservoirs producing above the bubble point. A term accounting for the change in water and formation volumes owing to their compressibilities is included in the material balance derivation, and the engineer can choose to eliminate this for particular applications. The gas in solution in the formation water is neglected, and in many instances, the volume of the produced water is not known with sufficient accuracy to justify the use of a formation volume factor with the produced water.
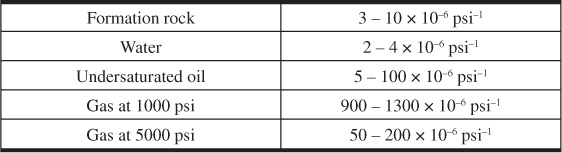
Table 3.1 Range of Compressibilities
The general material balance equation is simply a volumetric balance, which states that since the volume of a reservoir (as defined by its initial limits) is a constant, the algebraic sum of the volume changes of the oil, free gas, water, and rock volumes in the reservoir must be zero. For example, if both the oil and gas reservoir volumes decrease, the sum of these two decreases must be balanced by changes of equal magnitude in the water and rock volumes. If the assumption is made that complete equilibrium is attained at all times in the reservoir between the oil and its solution gas, it is possible to write a generalized material balance expression relating the quantities of oil, gas, and water produced; the average reservoir pressure; the quantity of water that may have encroached from the aquifer; and finally the initial oil and gas content of the reservoir. In making these calculations, the following production, reservoir, and laboratory data are involved:
1. The initial reservoir pressure and the average reservoir pressure at successive intervals after the start of production.
2. The stock-tank barrels of oil produced, measured at 1 atm and 60°F, at any time or during any production interval.
3. The total standard cubic feet of gas produced. When gas is injected into the reservoir, this will be the difference between the total gas produced and that returned to the reservoir.
4. The ratio of the initial gas cap volume and the initial oil volume, m:
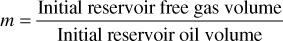
If the value of m can be determined with reasonable precision, there is only one unknown (N) in the material balance on volumetric gas cap reservoirs and two (N and We) in water-drive reservoirs. The value of m is determined from log and core data and from well completion data, which frequently helps to locate the gas-oil and water-oil contacts. The ratio m is known in many instances much more accurately than the absolute values of the gas cap and oil zone volumes. For example, when the rock in the gas cap and that in the oil zone appear to be essentially the same, it may be taken as the ratio of the net or even the gross volumes (without knowing the average connate water or average porosity).
5. The gas and oil formation volume factors and the solution gas-oil ratios. These are obtained as functions of pressure by laboratory measurements on bottom-hole samples by the differential and flash liberation methods.
6. The quantity of water that has been produced.
7. The quantity of water that has been encroached into the reservoir from the aquifer.
For simplicity, the derivation is divided into the changes in the oil, gas, water, and rock volumes that occur between the start of production and any time t. The change in the rock volume is expressed as a change in the pore volume, which is simply the negative of the change in the rock volume. In the development of the general material balance equation, the following terms are used:
N
Initial reservoir oil, STB
Boi
Initial oil formation volume factor, bbl/STB
Np
Cumulative produced oil, STB
Bo
Oil formation volume factor, bbl/STB
G
Initial reservoir gas, SCF
Bgi
Initial gas formation volume factor, bbl/SCF
Gf
Amount of free gas in the reservoir, SCF
Rsoi
Initial solution gas-oil ratio, SCF/STB
Rp
Cumulative produced gas-oil ratio, SCF/STB
Rso
Solution gas-oil ratio, SCF/STB
Bg
Gas formation volume factor, bbl/SCF
W
Initial reservoir water, bbl
Wp
Cumulative produced water, STB
Bw
Water formation volume factor, bbl/STB
We
Water influx into reservoir, bbl
c
Total isothermal compressibility, psi–1
Δ![]()
Change in average reservoir pressure, psia
Swi
Initial water saturation
Vf
Initial pore volume, bbl
cf
Formation isothermal compressibility, psi–1
The following expression determines the change in the oil volume:
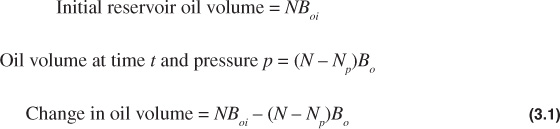
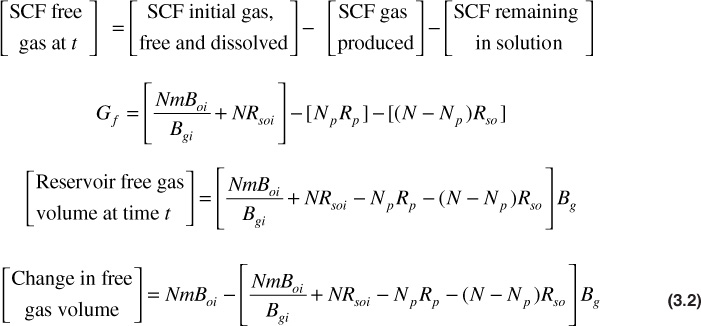
The following expression determines the change in free gas volume:
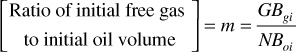
When initial free gas volume = GBgi = NmBoi,
The following expression determines the change in the water volume:
Initial reservoir water volume = W
Cumulative water produced at t = Wp
Reservoir volume of cumulative produced water = Bw Wp
Volume of water encroached at t = We
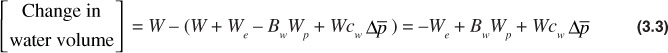
The following expression determines the change in the void space volume:
Initial void space volume = Vf
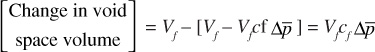
Or, because the change in void space volume is the negative of the change in rock volume,

Combining the changes in water and rock volumes into a single term yields the following:
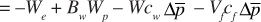
Recognizing that W = VfSwi and ![]() and substituting, the following is obtained:
and substituting, the following is obtained:
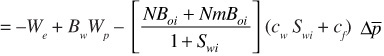
or
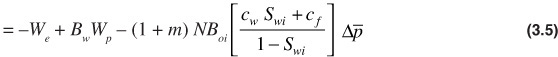
Equating the changes in the oil and free gas volumes to the negative of the changes in the water and rock volumes and expanding all terms produces
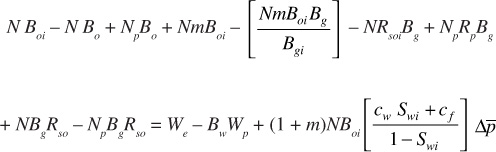
Adding and subtracting the term NpBgRsoi produces
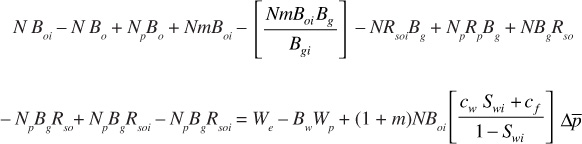
Then, grouping terms produces
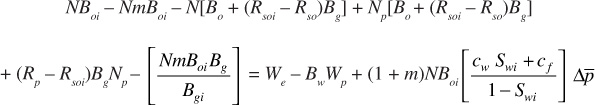
Writing Boi = Bti and [Bo + (Rsoi – Rso)Bg] = Bt, where Bt is the two-phase formation volume factor, as defined by Eq. (2.29), produces
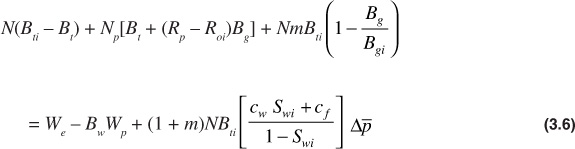
This is the general volumetric material balance equation. It can be rearranged into the following form, which is useful for discussion purposes:
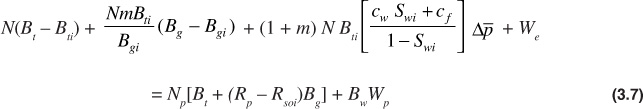
Each term on the left-hand side of Eq. (3.7) accounts for a method of fluid production, and each term on the right-hand side represents an amount of hydrocarbon or water production. For illustration purposes, Eq. (3.7) can be written as follows, with each mathematical term replaced by a pseudoterm:

The left-hand side accounts for all the methods of expansion or influx in the reservoir that would drive the production of oil, gas, and water, the terms on the right-hand side. Oil expansion is derived from the product of the initial oil in place and the change in the two-phase oil formation volume factor. Gas expansion is similar; however, additional terms are needed to convert the initial oil in place to initial gas in place—both free gas and dissolved gas. The third term can be broken down into three pieces. It is the product of the initial oil and gas in place, the expansion of the connate water and the formation rock, and the change in the volumetric average reservoir pressure. These three pieces account for the expansion of the connate water and the formation rock in the reservoir.
On the right-hand side, the oil and gas produced is determined by considering the volume of the produced oil if it were in the reservoir. The produced oil is multiplied by the sum of the two-phase oil formation volume factor and the volume factor of gas liberated as the pressure has declined. The produced water is simply the product of the produced water and its volume factor.
Equation (3.7) can be arranged to apply to any of the different reservoir types discussed. Without eliminating any terms, Eq. (3.7) is used for the case of a saturated oil reservoir with an associated gas cap. When there is no original free gas, such as in an undersaturated oil reservoir m = 0, and Eq. (3.7) reduces to
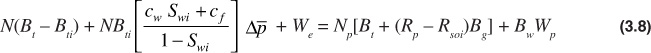
For gas reservoirs, Eq. (3.7) can be modified by recognizing that NPRP = Gp and NmBti = GBgi and substituting these terms into Eq. (3.7):
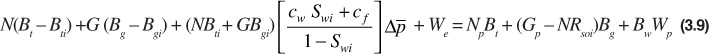
When working with gas reservoirs, there is no initial oil amount; therefore, N and Np equal zero. The general material balance equation for a gas reservoir can then be obtained:
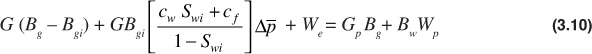
This equation is discussed in conjunction with gas and gas-condensate reservoirs.
In the study of reservoirs that are produced simultaneously by the three major mechanisms of depletion drive, gas cap drive, and water drive, it is of practical interest to determine the relative magnitude of each of these mechanisms that contribute to the production. Pirson rearranged the material balance Eq. (3.7) as follows to obtain three fractions, whose sum is one, which he called the depletion drive index (DDI), the segregation (gas cap) drive index (SDI), and the water-drive index (WDI).6
When all three drive mechanisms are contributing to the production of oil and gas from the reservoir, the compressibility term in Eq. (3.7) is negligible and can be ignored. Moving the water production term to the left-hand side of the equation, the following is obtained:
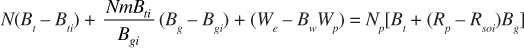
Dividing through by the term on the right-hand side of the equation produces
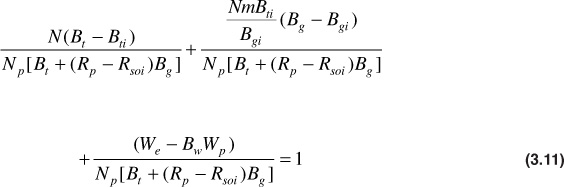
The numerators of the three fractions that appear on the left-hand side of Eq. (3.11) are the expansion of the initial oil zone, the expansion of the initial gas zone, and the net water influx, respectively. The common denominator is the reservoir volume of the cumulative gas and oil production expressed at the lower pressure, which evidently equals the sum of the gas and oil zone expansions plus the net water influx. Then, using Pirson’s abbreviations,
DDI + SDI + WDI = 1
Leave a Reply