Definition of the derivative

Consider a point x₀ and the increment ratio of function f at that point:

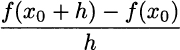
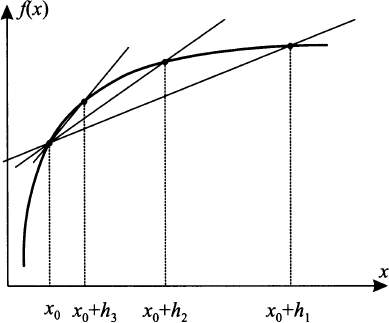
Fig. 2.17 The derivative is the limit of an increment ratio.

For a nonlinear function, keeping x₀ fixed, this ratio is a function of h. Now consider smaller and smaller steps h, as illustrated in Fig. 2.17. If we let h → 0, we get the “tangent” line to the graph of f at point x₀. The slope of this line is called the derivative of f at point x₀:

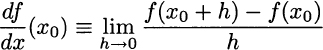
The notation reminds us that the derivative is the limit of the increment ratio Δf/Δx, when the step Δx becomes infinitesimal. We should also note that we may evaluate the derivative of a given function at several points. Indeed, taking the derivative of function f(x), we define another function. The notation

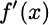
is also often used to indicate the derivative of f(x). Given the derivative, we may easily find the equation of the tangent line at any point on the graph of f(x). We recall that the equation of a line going through point (x₀, y₀), with slope m, is given by

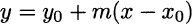
Hence, given the graph of f(x), we can express the tangent line at point (x₀, f(x₀)) as follows:

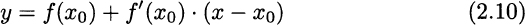
Example 2.16 In some easy cases, it is possible to find the derivative of a function by direct application of the definition. For instance, consider the quadratic function f(x) = x². Applying the definition, we have

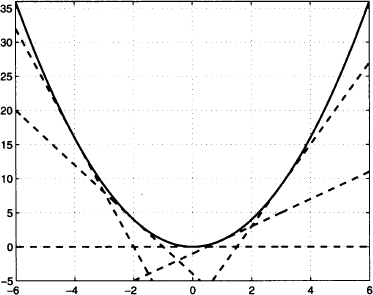
Fig. 2.18 The x² function and its tangent lines at points x₀ = −4, −2, 0, 1, 3.

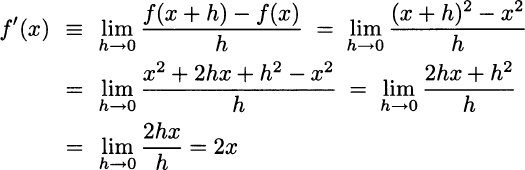
The key point here is that the expression 2hx + h² can be simplified for small values of h: A term like h² is negligible with respect to h, as it goes to zero at a faster rate. It is very useful to interpret the result by visualizing the plot of function x² and checking its derivative, as well as its tangent lines, as shown in Fig. 2.18. Analytically, the equation of the tangent lines, with slopes 2x₀ are given by straightforward application of Eq. (2.10):

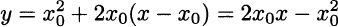
• For x₀ < 0, the derivative is negative. Indeed, the function is decreasing on the negative part of the real line, and the slope of the tangent line is negative. This slope goes to − ∞ when x₀ → −∞ and the rate at which the function decreases diminishes when x approaches zero.
• The derivative is zero for x₀ = 0; in fact, the tangent line there is horizontal.
• For positive values of x₀, the function is increasing; the rate of increase is itself increasing and it goes to infinity when x₀ → +∞.

The example shows that the derivative is quite useful in figuring out the behavior of a function. More generally, it can be shown that, for a positive integer n

This is a consequence of the binomial expansion formula (2.3). Consider the binomial (x + h)ⁿ for a small value of h

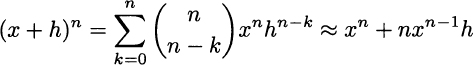
where the approximation is justified by the fact that higher powers of h are negligible when h → 0. Then, applying the definition of derivative, we get

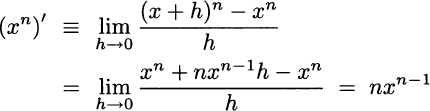
Later, we will see that Eq. (2.11) generalizes to an exponential function a^x, where x is a real number. Applying the result for n = 0, we see that the derivative of the constant function f(x) = 1 is zero. Alternatively, using the definition, it is easy to see that the derivative of any constant function is zero, since the increment of a constant function is identically zero.

More often than not, we do not apply the definition to find a derivative directly. Rather, we use a set of rules that are illustrated in Section 2.8, together with results about the derivative of basic functions, such as the exponential. But before doing that, it is important to realize that the derivative need not always exist.