Consider the ordinary limits of expected value and variance of the sample mean:
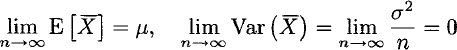
When variance goes to zero like this, intuition suggests that the probability mass gets concentrated and some kind of convergence occurs.
DEFINITION 9.9 (Convergence in quadratic mean to a number) If E[Xn] = μn and 
, and the ordinary limits of the sequence of expected values and variances are a real number β and 0, respectively, then the sequence Xn converges in quadratic mean to β.
Convergence in quadratic mean is also referred to as mean-square convergence, denoted as 
. Actually, the definition above is just a very specific case of the more general concept of rth mean convergence to a random variable.
DEFINITION 9.10 (Convergence in rth mean) Given r > 1, if the condition 
holds for all n, we say that the sequence Xn converges in rth mean to X if
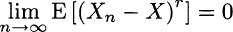
Not surprisingly, Definition 9.9 of mean-square convergence is equivalent to requiring
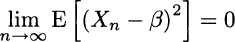
Convergence in quadratic mean implies convergence in probability, but the converse is not true, as illustrated by the following counterexample.
Example 9.30 Let us consider again the sequence of random variables of Example 9.29
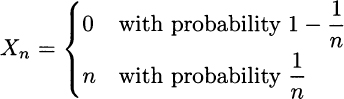
Whatever n we take, we have
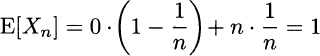
However, this contradicts the finding of Example 9.29, i.e., 
. Actually, we solve the trouble by noting this sequence does not converge in quadratic mean, since variance is not finite for n going to infinity:
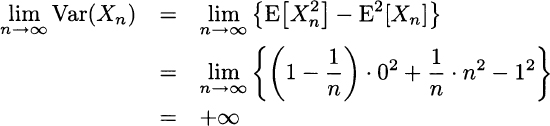
Leave a Reply