Convergence in distribution

We have already met convergence in distribution when dealing with the central limit theorem.

DEFINITION 9.11 (Convergence in distribution) The sequence of random variables X₁, X₂,…, with CDFs F_n(x), converges in distribution to random variable X with CDF F(x) if

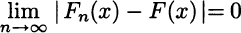
for all points at which F(x) is continuous.

Convergence in distribution can be denoted as

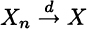
When convergence in distribution occurs, we may speak of a limiting distribution. The central limit theorem states that the limiting distribution of

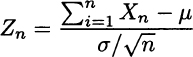
is the standard normal distribution. It is important to notice that convergence in distribution does not at all imply convergence to a constant. Furthermore, it can be shown that convergence in distribution is weaker than convergence in probability to a random variable, in the sense that

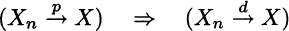
but the converse is not true.