CONTINUOUS FUNCTIONS

Before we proceed in our treatment of functions, we should pause a little and discuss a fundamental feature of functions: continuity, or lack thereof. Compare the graphs of polynomial functions in Fig. 2.8 against the graph of the rational function in Fig. 2.9. There is a striking qualitative difference between the two figures; in the first case, if we imagine drawing the plot with a pencil, we never “detach” the pencil from paper. In the second case, the function “jumps” from −∞ to +∞ and vice versa. Quite informally, it might be argued that if we can draw a graph without such interruptions, then the function is continuous.¹⁰ Lack of continuity may be the result of problems in the domain of the function, like the rational function above, which goes to infinity when we approach points where it is not defined, but this need not be the only case.

Example 2.9 Consider the following function:

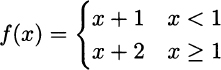
A qualitative plot of the function is depicted in Fig. 2.11. Please note the standard convention used in the figure: The filled bullet corresponds to the true value taken by the function for x = 1; the empty circle below corresponds to a value that is approached only when x gets close to 1 from the left, before the function jumps. If we get closer and closer to this critical point from the right, the value of the function tends to 3, which is indeed the value f(1) (please note the exact way in which the function is defined). We can express this by writing

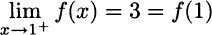
where x → 1⁺ denotes the fact that we approach x = 1 from the right, i.e., considering values like , where  gets smaller and smaller. An alternative notation is lim_x↓1. On the other hand, if we approach x = 1 from the left, we have a different limit:

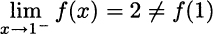
An alternative notation for this limit is lim_x↑1. We say that the function is continuous from the right, but discontinuous from the left.¹¹

The kind of discontinuity featured in the example is only one among the possible occurrences. In other situations, the trouble might stem from wild oscillations in the function, but we will not dwell too much in such pathological examples.¹²

DEFINITION 2.4 (Continuous function) A function f is said to be continuous at point x₀ if

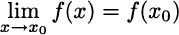
If this condition applies to all points within an interval or domain, we say that the function is continuous on that interval or domain.

We will not define the mathematical concept of limit too formally, as intuition suffices for our purposes.¹³ Still, you should note that convergence to a limit must be the same from both sides, left and right.