It turns out that Heisenberg’s uncertainty principle applies to pairs of observable things, and only to certain pairs. The technical name for these is conjugate pairs. We don’t need to go into all the conjugate pairs of observables or why they are conjugate, or even what in the world “conjugate” really means, but it will be useful to look at one more pair, energy and time. Energy and time are observable quantities which have the same uncertainty behavior as position and momentum.
DEFINITION
A conjugate pair of observables is a pair of quantities of a particle or system that obeys the Heisenberg uncertainty principle.
Let’s consider once again the concept of the wave packet. To construct a truly localized wave packet, you need a superposition of a large number of other waves, each with a slightly different wavelength. The interesting thing is that a certain range of different wavelengths near the average is required depending on how localized in position you want the resulting wave packet to be. Since wavelength is associated with momentum, we can also say that the wave packet is made up of waves with a range of momenta. In order to get a narrower spread in position, you need a wider range of momenta, and vice-versa.
We’ve been thinking of a wave packet spread out in position at a fixed point in time. Since the wave packet is moving, we could also view that wave packet at a fixed position over a range of times. After all, if I am located at a certain position, then when the wave packet passes I see an amplitude that varies with time.
From the time point of view, which we can call the time domain, we can construct a finite wave packet from a whole bunch of waves with slightly different frequencies. As you recall from our discussion of photons very early on, the energy of a particle is proportional to its frequency. In the time domain, then, the wave packet is made up of waves with a range of energies. If you want a narrower spread in time, you need to add in a wider range of energies. Conversely, if you can only add waves with a narrow range of energy (frequency) then the pulse will be more spread out in time.
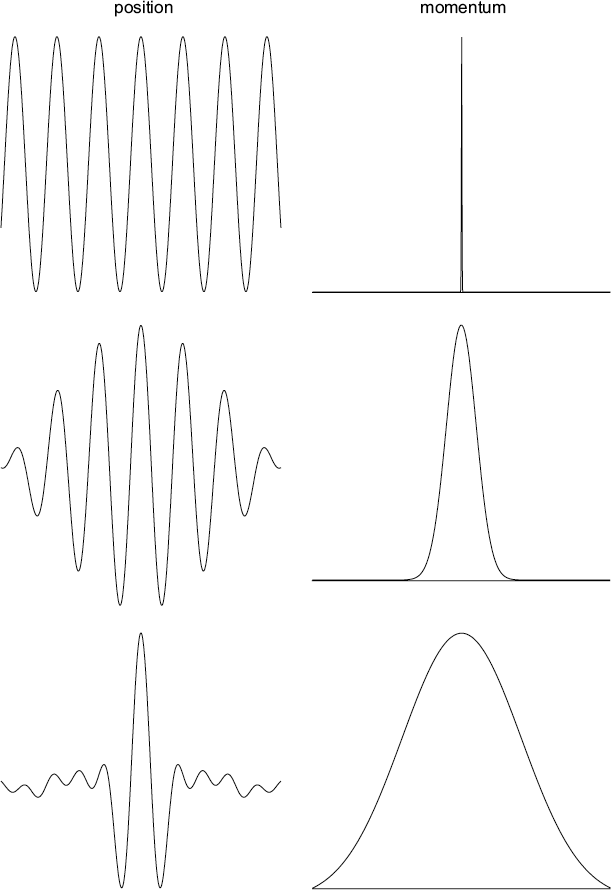
Here is an illustration of the position vs. momentum uncertainty trade-off. The left column shows the position of three different wave packets while the right column shows the corresponding range of momenta (wavelengths) used to construct them. When momentum is precisely defined, the position has maximum uncertainty. As the position becomes better defined, the range of momenta broadens.
Thus, uncertainties in energy and time measurements obey the same relationship as position and momentum. If we call the uncertainties ΔE and Δt, respectively, then Planck’s constant is once again the minimum value for their product: h < (ΔE × Δt). Energy and time form another conjugate pair of observables.
We called Δt the uncertainty in a time measurement, but a better way to think of it might be the duration in time of a certain state a particle is in. The sources of the radioactivity that we mentioned briefly are states of atoms and particles that we call unstable. We call them unstable because on average they only last for a finite time, after which they transform, or decay, to another state. That average time of existence of the initial state is usually called the lifetime.
DEFINITION
The lifetime is the average amount of time spent in the original state before a radioactive decay occurs. It is actually a statistical average, since we cannot say exactly when any specific particle or state will decay.
The Heisenberg uncertainty principle tells us that a state with a relatively short lifetime must also have a very uncertain energy (small Δt, large ΔE). In a sense, there isn’t enough time to know exactly what the energy of the state was before it decayed. Conversely, states that last a long time can have a more definite value for their energy. In the extreme limit, if the energy of a state is exactly determined (ΔE = 0) then it must have a lifetime that is infinitely long. We would call such a state “stable,” since it will never decay.
A stable state with a well-defined energy fits very well with our earlier description of electron energy levels in atoms. This is especially true for the low energy ones that are normally occupied by electrons unless a photon comes along to push them out to a higher orbit. On the other hand, going to infinity with either position or momentum uncertainty is less applicable to the real world. A precise momentum state would have to extend to infinity in space, which is not at all realistic. Neither can we imagine any realization of infinite momentum uncertainty for perfectly determined particle position.
Since mass is also a form of energy, the energy-time uncertainty leads to a couple other interesting quantum effects. The first is similar to the discussion of unstable states just above. Using ever-larger particle accelerators, high-energy physicists have discovered many more subatomic particles besides the electron, proton, and neutron that we are so familiar.
Most of these new particles are themselves unstable, decaying into other particles after a characteristic average lifetime. For such particles, the Heisenberg uncertainty principle tells us that they don’t even have a definite mass. The product of the mass uncertainty (multiplied by c2) with the lifetime can be no smaller than Planck’s constant. Therefore, unstable particles with very short lifetimes have relatively large uncertainties in their masses. There is a degree of randomness even in the masses of certain particles!

QUANTUM LEAP
In 1932, Heisenberg was awarded the Nobel Prize “for the discovery of quantum mechanics.” At the time, he was shocked that his colleagues Pascual Jordan and Max Born, with whom he had co-authored the seminal “three-man work” of 1926, did not share in the credit. For his part, Born was deeply saddened at having been overlooked by the Nobel committee. He was finally redeemed in 1954, however, when he was awarded his own Nobel Prize for his probabilistic interpretation of the wave function.
The second interesting effect is on the conservation laws that physicists hold so dear. Energy conservation, for example, can be violated, as long as the violation doesn’t last too long. Using Einstein’s mass-energy equivalence again, quantum mechanics allows a massive particle to spring into existence just about any place at any time, as long as it disappears within a time less than Δt.
If we take the mass and calculate the equivalent energy E=mc2, then as long as E times Δt is less than Planck’s constant, no biggie. Quantum physics predicts that such brief violations of mass-energy conservation can happen, and there is evidence in particle physics and astrophysics that it actually does happen all the time.
Leave a Reply