Considering a semicircle of radius R as shown in Figure 11.10. Due to symmetry centroid must lie on y-axis. Let its distance from the x-axis be 
. To find , consider an element at a distance r from the centre O of the semicircle, radial width dr, and bound by radii at θ and θ + dθ.
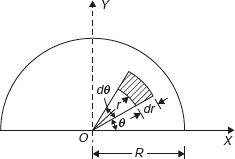
Figure 11.10 Centroid of Circular Section of a Disc
Area of the element = rdθ dr.
Its moment about x-axis is given by,
rdθ × dr × r sin θ = r2 sin θ dr dθ
Total moment of area about x-axis,
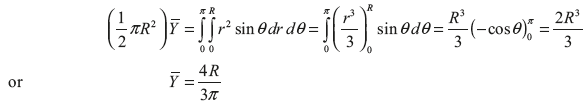
Thus, the centroid lies on y-axis at a distance of 
from the diametric axis.
Leave a Reply