Centre of Gravity, Centre of Mass, and Centroid of an Irregular Shape

In Figure 11.1, an irregular shape is shown for which we want to calculate the centre of gravity, centre of mass, and centroid. Here, our purpose is to differentiate the concepts of these three different terms. It is assumed that the irregular shape, as shown in Figure 11.1, is of uniform thickness, density, and subjected to uniform gravitational field.

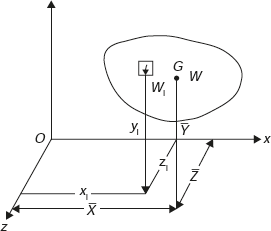
Figure 11.1 Centre of Gravity, Centre of Mass, and Centroid

Let W_i be the weight of an element in the given body. W be the total weight of the body. Let the coordinates of the element be X_i, Y_i, Z_i and that of centroid G be , , and . Since W is the resultant of W_i forces. Therefore,

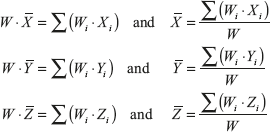
Here, , , and  are coordinates of centre of gravity, G. The resultant gravitational force acts through the point G.

If gravitational field be uniform, the gravitational acceleration (g) will be same for all the points. Therefore, in of W_i, we can put M_ig and the centre of mass can be expressed as

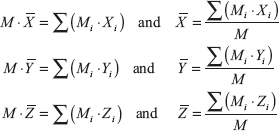
Here, , , and  are coordinates of centre of mass, G. The resultant mass of the body is concentrated at the point, G.

If the density of mass (γ) and the thickness of the body (t) is uniform, the mass M_i can be represented as γ × A_i × t. The centroid can be expressed as

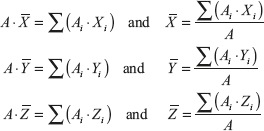
Here, , ,  and are coordinates of centroid, G.

11.2.2  Centroid of I-section

The I-section, shown in Figure 11.2, can be divided into three parts—lower part of area A₁, middle part of area A₂, and upper part of area A₃. The lengths and widths of all the parts of I-section are shown in Figure 11.2. Let the X and Y coordinates pass through origin O as shown in Figure 11.3.

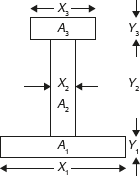
Figure 11.2 Centroid of I-section

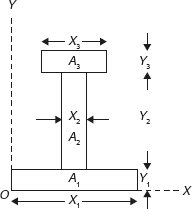
Figure 11.3 Reference Axes for I-section

The coordinates for centroid can be calculated using the following formula:

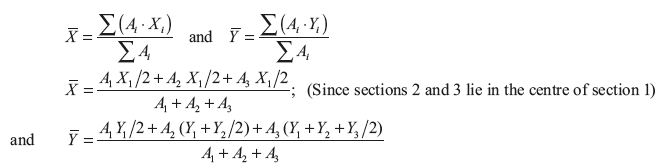
In the case of axial symmetry about Y-axis (i.e., y-axis passes through centres of sections 1, 2 and 3), the distances of X₁/2, X₂/2, X₃/2 from origin will be zero.

Hence,  = 0.