One of the important functions of the reservoir engineer is the periodic calculation of the reservoir oil (and gas) in place and the recovery anticipated under the prevailing reservoir mechanism(s). In some companies, this work is done by a group that periodically renders an account of the company’s reserves together with the rates at which they can be recovered in the future. The company’s financial position depends primarily on its reserves, the rate at which it increases or loses them, and the rates at which they can be recovered. A knowledge of the reserves and rates of recovery is also important in the sale or exchange of oil properties. The calculation of reserves of new discoveries is particularly important because it serves as a guide to sound development programs. Likewise, an accurate knowledge of the initial contents of reservoirs is invaluable to the reservoir engineer who studies the reservoir behavior with the aim of calculating and/or improving primary recoveries—for it eliminates one of the unknown quantities in equations.
Oil reserves are usually obtained by multiplying the oil in place by a recovery factor, where the recovery factor is the estimated fraction of the oil in place that will be produced through a particular production or reservoir drive mechanism. They can also be estimated from decline curve studies and by applying appropriate barrel-per-acre-foot recovery figures obtained from experience or statistical studies of well or reservoir production data. The oil in place is calculated either (1) by the use of geological, geophysical, and fluid property data or (2) by material balance studies, both of which were presented for gas reservoirs and will be given for oil reservoirs in this and following. In the latter case, recovery factors are determined from (1) displacement efficiency studies and (2) correlations based on statistical studies of particular types of reservoir mechanisms.
The first method for estimating oil in place starts with an estimate of the bulk reservoir volume using the techniques considered. Then log and core analysis data are used to determine the bulk volume, porosity, and fluid saturations, and fluid analysis data are used to determine the oil volume factor. Under initial conditions, 1 ac-ft of bulk oil productive rock contains the following:
where 7758 barrels is the equivalent of 1 ac-ft, φ is the porosity as a fraction of the bulk volume, Sw is the interstitial water as a fraction of the pore volume, and Boi is the initial formation volume factor of the reservoir oil. Using somewhat average values (φ = 0.20, Sw = 0.20, and Boi = 1.24), the initial stock-tank oil in place per acre-foot is on the order of 1000 STB/ac-ft, or
For oil reservoirs under volumetric control, there is no water influx to replace the produced oil, so it must be replaced by the swelling of the oil phase or expanding gas, the saturation of which increases as the oil saturation decreases. If Sg is the gas saturation and Bo the oil volume factor at abandonment, then at abandonment conditions, 1 ac-ft of bulk rock contains the following:
Then the recovery in stock-tank barrels per acre-foot is
and the fractional recovery in terms of stock-tank barrels is
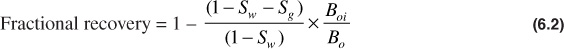
The total free gas saturation to be expected at abandonment can be estimated from the oil and water saturations as reported in core analysis.7 This expectation is based on the assumption that, while being removed from the well, the core is subjected to fluid removal by the expansion of the gas liberated from the residual oil and that this process is somewhat similar to the depletion process in the reservoir. In a study of the well-spacing problem, Craze and Buckley collected a large amount of statistical data on 103 oil reservoirs, 27 of which were considered to be producing under volumetric control.8,9 The final gas saturation in most of these reservoirs ranged from 20% to 40% of the pore space, with an average saturation of 30.4%. Recoveries may also be calculated for depletion performance from a knowledge of the properties of the reservoir rock and fluids.
In the case of reservoirs under hydraulic control, where there is no appreciable decline in reservoir pressure, water influx is either inward and parallel to the bedding planes, as found in thin, relatively steep dipping beds (edgewater drive), or upward where the producing oil zone (column) is underlain by water (bottomwater drive). The oil remaining at abandonment in those portions of the reservoir invaded by water, in barrels per acre-foot, is as follows:
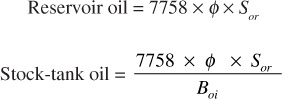
where Sor is the residual oil saturation remaining after water displacement. Since it was assumed that the reservoir pressure was maintained at its initial value by the water influx, no free gas saturation develops in the oil zone, and the oil volume factor at abandonment remains Boi. The recovery by active water drive then is
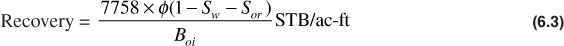
and the recovery factor is

It is generally believed that the oil content of cores, reported from the analysis of cores taken with a water-based drilling fluid, is a reasonable estimation of the unrecoverable oil because the core has been subjected to a partial water displacement (by the mud filtrate) during coring and to displacement by the expansion of the solution gas as the pressure on the core is reduced to atmospheric pressure.10 If this figure is used for the resident oil saturation in Eqs. (6.3) and (6.4), it should be increased by the formation volume factor. For example, a residual oil saturation of 20% from core analysis indicates a residual reservoir saturation of 30% for an oil volume factor of 1.50 bbl/STB. The residual oil saturation may also be estimated using the data of Table 4.2, which should be applicable to residual oil saturations as well as gas saturations (i.e., in the range of 25% to 40% for the consolidated sandstones studied).
In the reservoir analysis made by Craze and Buckley, some 70 of the 103 fields analyzed produced wholly or partially under water-drive conditions, and the residual oil saturations ranged from 17.9% to 60.9% of the pore space.8 According to Arps, the data apparently relate according to the reservoir oil viscosity and permeability.7 The average correlation between oil viscosity and residual oil saturation, both under reservoir conditions, is shown in Table 6.2. Also included in Table 6.2 is the deviation of this trend against average formation permeability. For example, the residual oil saturation under reservoir conditions for a formation containing 2 cp oil and having an average permeability of 500 md is estimated at 37 + 2, or 39% of the pore space.
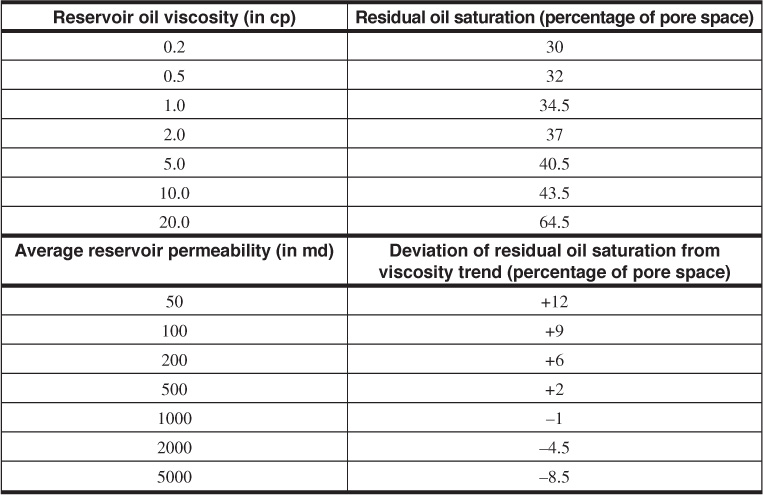
Table 6.2 Correlation between Reservoir Oil Viscosity, Average Reservoir Permeability, and Residual Oil Saturation (after Craze and Buckley and Arps)7,8
Because Craze and Buckley’s data were arrived at by comparing recoveries from the reservoir as a whole with the estimated initial content, the residual oil calculated by this method includes a sweep efficiency as well as the residual oil saturation—that is, the figures are higher than the residual oil saturations in those portions of the reservoir invaded by water at abandonment. This sweep efficiency reflects the effect of well location, the bypassing of some of the oil in the less permeable strata, and the abandonment of some leases before the flooding action in all zones is complete, owing to excessive water-oil ratios, in both edgewater and bottomwater drives.
In a statistical study of Craze and Buckley’s water-drive recovery data, Guthrie and Greenberger, using multiple correlation analysis methods, found the following correlation between water-drive recovery and five variables that affect recovery in sandstone reservoirs.11
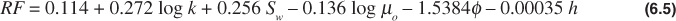
For k = 1000 md, Sw = 0.25, μo = 2.0 cp, φ = 0.20, and h = 10 ft,
RF = 0.114 + 0.272 × log 1000 + 0.256 × 0.25 – 0.136
log 2 – 1.538 × 0.20 – 0.00035 × 10
0.642, or 64.2% (of initial stock-tank oil)
where
RF = recovery factor
A test of the equation showed that 50% of the fields had recoveries within ± 6.2% recovery of that predicted by Eq. (6.5), 75% were within ± 9.0% recovery, and 100% were within ± 19.0% recovery. For instance, it is 75% probable that the recovery from the foregoing example is 64.2 ± 9.0%.
Although it is usually possible to determine a reasonably accurate recovery factor for a reservoir as a whole, the figure may be wholly unrealistic when applied to a particular lease or portion of a reservoir, owing to the problem of fluid migration in the reservoir, also referred to as lease drainage. For example, a flank lease in a water-drive reservoir may have 50,000 STB of recoverable stock-tank oil in place but will divide its reserve with all updip wells in line with it. The degree to which migration may affect the ultimate recoveries from various leases is illustrated in Fig. 6.1.12 If the wells are located on 40-acre units, if each well has the same daily allowable, if there is uniform permeability, and if the reservoir is under an active water drive so that the water advances along a horizontal surface, then the recovery from lease A is only one-seventh of the recoverable oil in place, whereas lease G recovers one-seventh of the recoverable oil under lease A, one-sixth under lease B, one-fifth under lease C, and so on. Lease drainage is generally less severe with other reservoir mechanisms, but it occurs to some extent in all reservoirs.
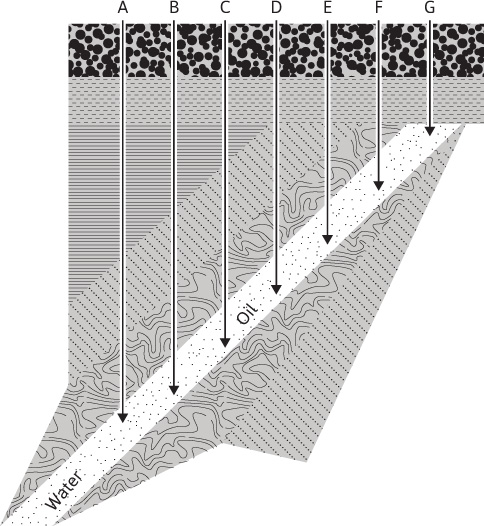
Figure 6.1 Effect of water drive on oil migration (after Buckley, AlME).12
Leave a Reply