Using the definition above to compute an integral is cumbersome, to say the least. It may work in some simple cases, but we certainly need something more handy. Luckily, the following theorem, which really deserves the name fundamental,27 provides us with a practical way to compute definite integrals.
THEOREM 2.22 (Fundamental theorem of calculus) Let F(x) be a function such that F′(x) = f(x), and assume that f is continuous on the interval [a, b]. Then
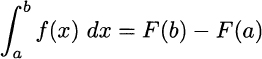
Function F is called the antiderivative of f. Actually, if F is the antiderivative of f, this also holds for any function F(x) + C obtained by adding an arbitrary constant C. However, since in the theorem we take the difference F(b) − F(a), the constant is irrelevant. The following shorthand notation is used:
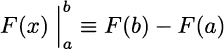
Example 2.41 To illustrate the theorem, recall that (x2)′ = 2x. Then, if we consider f(x) = x, its antiderivative is F(x) = x2/2 (plus an irrelevant constant):
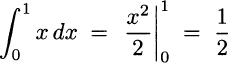
which is indeed the area of the triangle associated with the function f(x) = x on interval [0, 1].
Armed with the fundamental theorem, we are certainly able to compute integrals of relatively simple functions formed using powers and exponentials. Sometimes, quite ingenious tricks are needed to find the antiderivatives of intricate functions, but we will not need that for what follows. The next property of definite integrals is quite helpful in dealing with sums of functions.
PROPERTY 2.23 If α and β are arbitrary real numbers and all of the integrals below exist, then
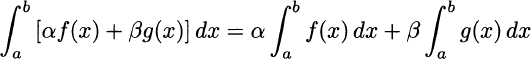
As you may imagine, this property is linked to the similar properties of derivatives.28
Example 2.42 Consider function f(x) = x2 + 1 − 3e−2x, to be integrated on interval [0, 4]. It is easy to see that the antiderivative of x2 + 1 is x3/3 + x. The exponential is a bit trickier, but we may recall that
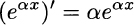
So, the antiderivative of −3e−2x is 3e−2x/2, and the integral is
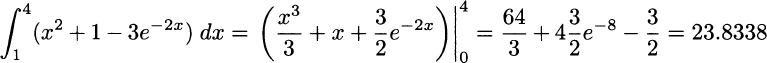
Leave a Reply