Rydberg had been able to capture the observed periodicity of the hydrogen lines in an elegant formula, but he had no idea what underlying physical process could be responsible for such mathematical regularity.
Returning to 1911, we find the world of physics was faced with a major riddle about the atomic structure proposed by Rutherford. The three major questions were:
1. Why don’t electrons fall into the nucleus?
2. Why don’t atoms emit light in a continuous spectrum containing all colors?
3. Why do atoms emit light only at specific wavelengths unique to each element?
Enter Danish physicist Niels Bohr—Rutherford’s new, young assistant at Manchester University. Bohr asked himself if the quantization that had been used by Planck to solve the blackbody radiation problem and by Einstein to explain the photoelectric effect was in fact a universal characteristic of energy. That is, maybe the emission or absorption of energy by any material object could only take place in discrete jumps, and never as a gradual, smooth change. If this were the case for Rutherford’s atom, then very small changes in the electron’s energy would be impossible, and the electron would remain trapped in its orbit.
Taking this idea further, Bohr boldly proposed that there are only certain stable orbits in which the electron can exist without crashing into the nucleus after spiraling to its death. Bohr restricted the allowed orbits to those in which the energy would be quantized into a value proportional to integer steps of h—the constant Planck had determined as the smallest quantum.‡
The assumption that only certain orbits would be allowed led Bohr to propose that an electron moving from one allowed orbit to another would either need to absorb or emit a certain quantized amount of energy.
So for the hydrogen atom shown in Figure 83, Bohr proposed that an electron would radiate a photon as it jumped from a higher orbit E2 to a lower orbit E1. The photon would then carry an amount of energy equal to the loss of energy by the electron when jumping between these orbits:
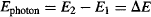
Figure 83 In the Bohr model of the hydrogen atom, electrons are allowed to circulate around the nucleus only at very specific orbits. Jumping from a higher orbit to a lower orbit causes the emission of a photon that carries the difference in energy between the two orbits.
Remember that Einstein had discovered during his work on the photoelectric effect that the energy of a photon is equal to Planck’s constant multiplied by the photon’s frequency, so Bohr substituted Ephoton = hf into the prior equation to obtain:
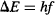
Bohr kept on exploring the math of his atom model, and through quite simple arithmetic and basic physics was able to arrive at Rydberg’s constant just from the balance of energy lost by the electron when it jumped between allowed orbits! Remember that Rydberg arrived at his constant by fitting a formula to experimental data, but without any knowledge of the processes that generated the spectral lines. In contrast, Bohr arrived at the same constant from a purely theoretical basis, and demonstrated that Rydberg’s constant can be derived from more fundamental constants:
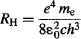
where
ε0 = 8.854 × 10−12 A · s/V · m is the permittivity of free space, which is a constant that relates the mechanical force between two separated electric charges (in our case the electron and the nucleus) to the amount of charge they carry (in our case the absolute value of charge for the electron and the nucleus is the same),
e = 1.602 × 10−19 Coulomb is the charge of the electron (and the nucleus),
me = 9.109 × 10−31 kg is the mass of the electron,
c = 299,792,458 m/s is the speed of light, and
h = 6.626 × 10−34 J · s is Planck’s constant.
Go ahead—take out your calculator and check if plugging the values of these fundamental constants results in the value that Rydberg found empirically. By the way, you may need to first simplify some of the powers of 10, since most calculators will round up h3 to zero and won’t let you make that division.
Bohr’s achievement was astonishing. His model of the hydrogen atom behaved like the real thing, being able to predict the entire emission spectrum of the hydrogen atom based on fundamental physics plus the assumption of quantization! Bohr was later awarded the 1922 Nobel Prize in Physics “for his services in the investigation of the structure of atoms and of the radiation emanating from them.”
Leave a Reply