The Bernoulli’s equation is an approximate relation between pressure, velocity and elevation, and is valid in regions of steady and incompressible flow where net frictional forces are negligible. Despite its simplicity, it has proven to be a very useful tool in fluid mechanics. The key approximation in the derivation of the Bernoulli equation is that viscous effects are negligibly small compared to inertial, gravitational and pressure effects. Since all fluids have viscosity, this approximation cannot be valid for an entire flow field of practical interest. In other words, we cannot apply the Bernoulli equation everywhere in a flow, no matter how small the fluid’s viscosity. However, it turns out that the approximation is reasonable in certain regions of many practical flows. We refer to such regions as inviscid regions of flow, and we stress that they are not regions where the fluid itself is inviscid or frictionless, but rather they are regions where net viscous or frictional forces are negligibly small compared to other forces acting on fluid particles.
Considering a stream-line flow takes place in s direction as shown in Figure 9.5. A small element of fluid of cross-sectional area dA and length ds is considered for force analysis. The forces acting on this element are given as follows:
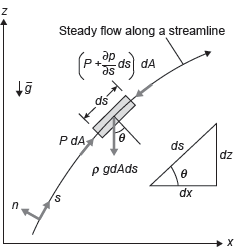
Figure 9.5 Forces on Fluid Element
- Pressure force, pdA in the direction of flow.
- Pressure force
 opposite to the direction of flow.
opposite to the direction of flow. - Weight of the fluid element, ρgdAds.
The resultant force on the fluid element in the direction of flow must be equal to the Mass of fluid element × Acceleration in the direction.
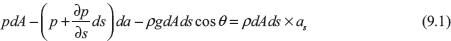
where as is acceleration in direction s.
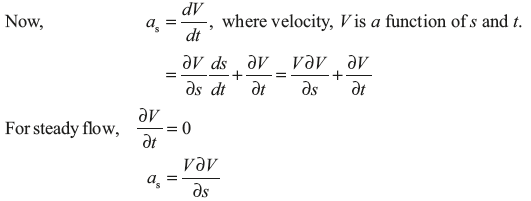
Putting the value of as in Eq (9.1), we get
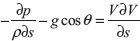
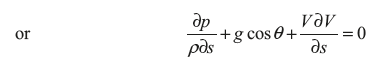
Therefore,
Putting the value of  from Figure 5.5b
from Figure 5.5b
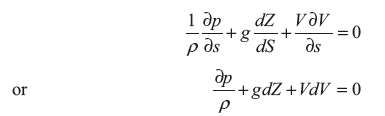
This is known as Euler’s equation of motion.
Bernoulli’s equation is obtained by integrating the Euler’s equation of motion.
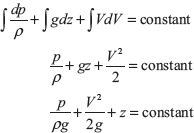
where ![]() represents the pressure energy per unit weight
represents the pressure energy per unit weight
![]() represents the kinetic energy per unit weight
represents the kinetic energy per unit weight
z represents the kinetic energy per unit weight
Example 9.5: The water is flowing through a pipe having diameters 30 and 20 cm at two sections 1 and 2, respectively. The rate of flow through pipe is 80 l/s. The section 1 is 8 m above the datum and section 2 is 5 m above the datum. If pressure at section 1 is 4 bar, find the intensity of pressure at section 2.
Solution:
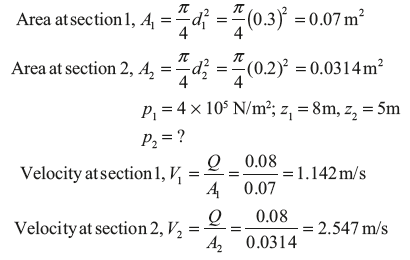
From Bernouilli’s equation, we get
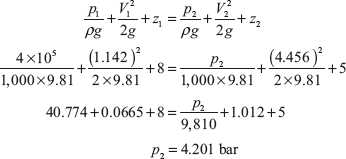
Leave a Reply