Preoccupied by the lead-up and aftermath of the Second World War, physicists temporarily set aside further attempts to figure out the more esoteric implications of quantum physics. The next big step had to wait for the Irish physicist John Bell to take a sabbatical year in 1964.
Bell had long been interested in the strangeness of quantum mechanics, but it wasn’t until he got away from his normal research work that he could fully indulge his curiosity and explore the question of hidden variables. The problem with the EPR paradox was that it was basically an intellectual exercise. It relied on logic, and did not suggest any experimental way to determine which of the competing interpretations was correct. Einstein and Bohr had different interpretations of the scenario, but both would agree that the two observers would make the same measurements regardless of the interpretation.
Bell set his mind to remedying this situation. His tactic was to make some adjustments to the EPR Gedankenexperiment, and come up with a solid prediction that might be testable. Instead of assuming the Copenhagen interpretation was correct, he set out to predict what would happen if there really were a hidden variable that predetermined the outcome of the measurements. Bell’s argument actually started with two assumptions, very closely related to Einstein’s ideas of objective reality and the locality of physical laws.
Bell also started with an entangled two-particle system, in which the two particles start off from a common location. The spin states of each particle are then measured at distant locations. Bell’s argument does not depend on exactly what physical property we use, but his first assumption is that this property is real, in the sense that it is not created or influenced by any act of measurement. The second assumption may be called “separability.” It says that when the two objects are physically separated from one another, they can’t affect each other in any way. Any hidden variable in this scenario would therefore have to obey the principle of locality; it would be a local hidden variable.

DEFINITION
A local hidden variable is some unknown (hidden) mechanism that predetermines the outcome of measurements but whose influence cannot travel faster than the speed of light.
As a concrete example, let’s consider a steady flow of entangled electrons and ask what a pair of observers would find (on average) after making a whole bunch of spin state measurements. As we have seen, the direction of electron spin is quantized with respect to any arbitrarily chosen axis, or direction in space. Since the spin quantum number of the electron is 1⁄2, there are only two possible measurement outcomes, which we have been calling up and down. During our discussion of the EPR experiment, we implicitly assumed that both measurements (at A and B) were made along the same axis. For now, we will call that selected axis vertical. In that case, quantum mechanics predicted that the two observers would see opposite spin directions 100 percent of the time.
Now we let the observer at B rotate his measurement axis (i.e., rotate the orientation of his Stern-Gerlach magnet) about the direction of the electron’s motion. When his measurement access is vertically upward, we have the previous case and his or her measurements are exactly opposite those at point A. When e1 is found to be up, e2 is found to be down (and vice-versa). Since the measurements give opposite results, we say they are anticorrelated and can assign a value of -1 to the correlation.
At the other extreme, when the measurement axis at B is rotated 180 degrees so that it points vertically downward, we see that the two observers actually detect the same spin. When e1 is found to be up at point A, then e2 will always be found pointing up at point B. The spins are still pointing in opposite directions (conservation of angular momentum), but since our measurement apparatus at B is standing on its head, it detects the same spin as the measurement at A. Now the measurements give the same results, and we say they are correlated. We can assign a value of +1 to the correlation.
Now we rotate the Stern-Gerlach magnet at B by 90 degrees, so that it is pointing horizontally. The results here are a little more unusual. Because the two detectors are exactly perpendicular to one another, we find that our measurements at B are randomly up or down (relative to the horizontal measurement access), regardless of the outcome of the measurement at A. In this case, half of the measurements give the same result (correlation = +1) and half give the opposite result (correlation = -1). If we take the average of a bunch of measurements, all the positive and negative ones average out to exactly 0. The correlation with a horizontal magnet at B is zero.
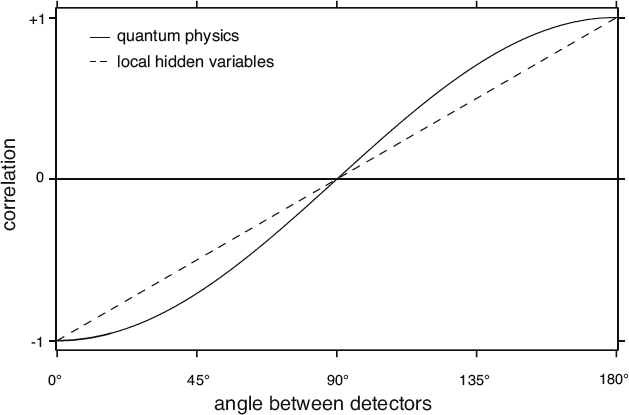
Here is a comparison of the degree of correlation for two distant measurements of entangled spin states if we allow the presence of local hidden variables versus that predicted by quantum physics.
The results obtained for these three cases would be the same whether you believed the probabilistic interpretation of quantum physics or whether you allowed for a local hidden variable to predetermine the outcome of the measurements. For all other angles, however, it turns out that the quantum physics view and the local hidden variables view give different answers.
Bell worked out the math for the correlation that our two observers would measure for any arbitrary angle between the two detectors. If he assumed the presence of some local hidden variable, the correlation would vary from -1 to +1 in a straight line as the angle between the detectors went from 0 degrees to 180 degrees. Moreover, he concluded that in the presence of a local hidden variable, the correlation of certain pairs of measurements would have to satisfy a specific mathematical relationship that we now call Bell’s inequality.
DEFINITION
Bell’s inequality is a mathematical relationship between certain correlated measurements that is satisfied in the presence of local hidden variables.
The standard quantum physics prediction was different, however. If we assume the quantities have no real values until they are measured, and that a measurement of e1 instantaneously influences e2, then we would get a larger degree of correlation at all the in-between detector angles. This implies that the standard quantum physics prediction violates Bell’s inequality, meaning the two original assumptions could not both be true. If the quantum physics prediction actually happened, it would mean that either there was no hidden variable, or the particles were not separable, or both.
ATOM TRAP
Given that Bell’s inequality is used as a test of quantum physics, it is tempting to think that a measurement in support of quantum physics would satisfy Bell’s inequality. However, given that Bell’s logic started by assuming the presence of local hidden variables, it turns out that measurements in support of quantum physics are those that violate Bell’s inequality.
What’s more, the appearance of Bell’s inequality finally gave experimental quantum physicists something to shoot at. If they could set up experiments that violated Bell’s inequality, then they could finally do away with the possibility of local hidden variables and provide strong support for the completeness of quantum physics.
Leave a Reply