We’ve just demonstrated that quantum particles can actually seep into classically forbidden regions. We’ll delve into the philosophical aspects of that soon enough, but for now we simply ask, could this strange behavior actually be detected in the laboratory?
To answer that, let’s consider a slightly different case–that of a potential “wall” instead of a well. Imagine a case where the potential energy is zero everywhere except for some narrow range of x. Within that range, we will give the potential energy some positive value.
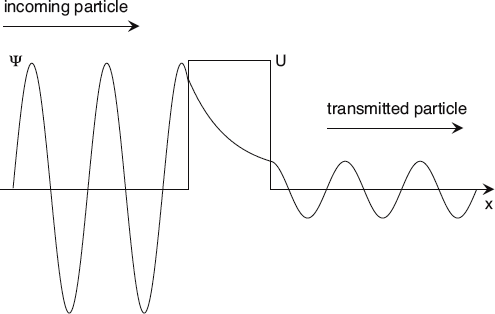
Unlike classical particles that bounce off of walls, quantum particles can burrow right through. The likelihood of this occurrence depends on incoming particle’s energy and the size of the barrier itself.
Now, imagine a particle approaching from the left of the barrier. In this region (and a long, long way off to the left) the potential energy is a constant zero, so the free particle, plane wave solutions can have any possible energy, according to the Schroedinger equation. Let’s pick one of these solutions where the wave is moving to the right, and the particle has an energy that is a little less than the potential energy of the barrier.
To find out what happens to this incoming wave when it collides with the wall, we would use the same technique we used when we dealt with square potential wells. As before, there are three different regions along the x-axis, with different constant values of the potential energy. We’d solve the Schroedinger equation separately in the three regions, then choose solutions that we can match up at the boundaries, matching both the value of the wave function and its slope at each boundary.
Since the particle’s energy is less than the potential energy within the barrier, the barrier corresponds to another one of those classically forbidden regions we defined earlier. In such regions, we can’t have oscillating solutions like we have when the total energy is greater than the potential. Inside the barrier, only exponentially decaying wave functions satisfy the Schroedinger equation. So working from the left, we have to match an oscillating plane wave function to a decaying exponential at the first boundary. So far, nothing new.
Now comes the interesting part. The barrier is only so wide. The exponential wave function is decreasing from left to right, but it is not quite zero at the right edge of the barrier. In order to have a complete solution, we have to come up with another wave function for the region to the right of the barrier. Since the potential energy is zero again here, we will need another plane wave, and its value and slope must match up with that of the decaying wave function at this boundary as well.
What does this mean? It means that for a particle incident from the left, there is a small but real probability that the particle will actually pass through the barrier and continue moving to the right! This never happens in classical physics, since the barrier region is forbidden, after all. It can happen only in the quantum realm.
The probability of penetration, or “tunneling” as it’s known, depends critically on both the width and the height of the barrier. Obviously, the wider the barrier, the smaller the amplitude of the wave that will match on the right. This means the probability of tunneling gets really small as the barrier widens. Also, the higher the barrier, the faster the exponential function decays, which again reduces the amplitude of the wave function on the right.
QUANTUM LEAP
Quantum tunneling was observed as far back as the 1960s. It was in 1962, in fact, that British physicist Brian David Josephson correctly explained some weird electron behavior in sensitive electronic circuits as just the effect we have described. The Josephson effect and Josephson junctions are named after him, and he picked up a Nobel Prize for his efforts to boot. Superconductivity makes these effects even more pronounced and easier to exploit devoted to real applications of quantum physics.
Leave a Reply