Principal component analysis can be applied in a marketing setting when questionnaires are administered to potential customers asking for a quantitative evaluation along many dimensions. Many such questions are, or are perceived as, redundant. Spotting the few principal components may help in assessing which product features, or combination thereof, are most important. They can also tell groups of customers apart, helping in market segmentation.
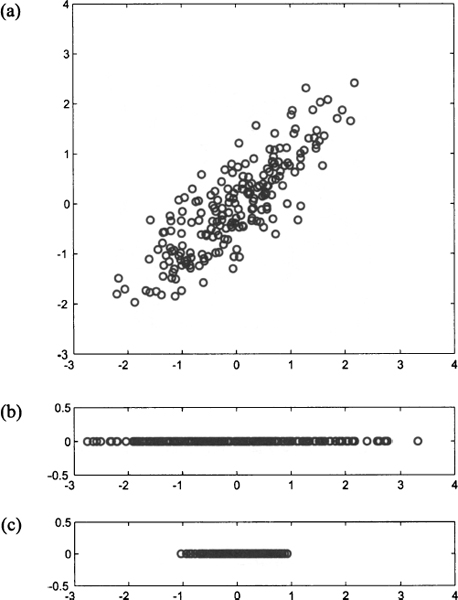
Fig. 17.3 PCA on sampled data.
PCA can be applied in a financial setting as well, to reduce the dimensionality of the term structure of interest rates, which specifies an interest rate for different time periods. Let Rt,t+T be the annualized interest rate for a loan starting at time t and maturing at time t + τ, where τ is the length of corresponding time period. Usually, such rates are not constant and are increasing with τ. There are different theories trying to explain the term structure; one of the possible explanations is based on liquidity risk, which is higher for longer maturities. If we observe these rates over time, they are going to change randomly. However, such changes must preserve some basic consistency between rates, in order to prevent arbitrage opportunities. Measuring and managing interest rate risk is complicated by the presence of so many interrelated risk factors; also Monte Carlo simulation can be challenging. One possible approach to make the problem more manageable is to replace the term structure by a few key risk factors, possibly obtained by PCA.6
Leave a Reply