One of the most fruitful application fields of quantitative methods is revenue management. Revenue management is actually a group of techniques that can be applied in quite diverse settings, such as pricing of aircraft seats or perishable products. In this section we consider an idealized case in which a manufacturer has to find an optimal price for the items she produces and sells. We have to clarify the context in which she operates, however, as one cannot really set prices at will if there is stiff competition. To keep it as simple as possible, let us assume that there is no competition at all; the manufacturer is a monopolist The fact that there is no competition does not imply that one can set arbitrarily high prices, since doing so will just kill demand. Indeed, the monopolist, barred other “political” constraints, must find the best tradeoff between the conflicting needs of selling as much as possible and setting as high a price as possible. This is a classical problem in microeconomics.
The first step to cope with our task is to find a suitable formalization. We want to maximize profit, which is revenue minus cost. The total cost depends on the manufactured amount q. Hence, it is a function TC(q). As an example, we might consider a cost function
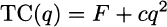
where F is a fixed cost and the variable cost component involves a squared term; in such a model, cost increases rather rapidly for large values of q, reflecting possible inefficiencies in large-scale production.
We also need to find a relationship between price and demand. Usually, one would expect that an increase in price implies a drop in demand. One possible model of that is a demand function such as
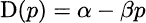
expressing demand as a function of price p, with β > 0. This linear demand function is just a simplistic model used for illustration; it is clearly valid on only a limited range, as for suitably large prices it would imply a negative demand. In practice, one would use statistical tools described in later to analyze data and identify such a relationship on an empirical basis. One problem we have is that cost is naturally expressed as a function of q, whereas demand is expressed as a function of price. Since cost depends on the produced amount, it is convenient to express everything as a function of q, which calls for inversion of the demand function:
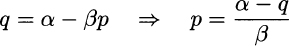
Hence, we define the inverse demand function, expressing price as a function of quantity
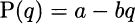
where a ≡ α/β and b ≡ 1/β. Now we are finally able to express our problem. Profit Π(q) is the difference between revenue R(q) and cost TC(q). Since revenue in turn is just price times demand, the profit maximization problem is as follows:
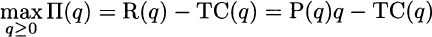
We will disregard the nonnegativity constraint on the decision variable q; we assume an interior solution, which we may check after solving the problem. Revenue as a function of quantity is
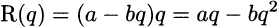
We could just apply the stationarity condition Π′(q) = 0 to the profit function, but it is more instructive to take an alternative but equivalent route that yields a better understanding of the economics involved. The first-order optimality condition can be written as
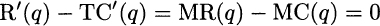
where MR(q) and MC(q) are called the marginal revenue and marginal cost, respectively. Marginal revenue, which is just the derivative of revenue with respect to quantity, tells us the rate at which revenue increases if we increase quantity; by the same token, marginal cost is the rate at which total cost increases when increasing production. The optimality condition tells us that marginal revenue should equal marginal cost, and it is quite instructive to interpret this condition:
- If marginal revenue is larger than marginal cost, then we should increase production, since revenue increases faster than cost.
- If marginal revenue is smaller than marginal cost, then we should decrease production, since cost decreases faster than revenue.
- The optimal production corresponds to an amount q* such that there is no reason to either increase or decrease production.
Using our simplistic model, we have
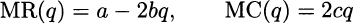
and the first-order optimality condition reads as follows:

Note that, indeed, we get an interior solution q* > 0; hence, the nonnegativity constraint is not binding and we verify ex post that it can be disregarded. Then, the optimal price is
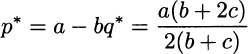
Since all of the involved parameters are nonnegative, optimal price is nonnegative as well. It is also easy to check that
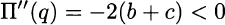
so we really found a minimizer.
The fixed cost F did not play any role in the analysis and this is consistent with what we pointed out in Section 1.1.1. A constant term, which is not affected by q, does not influence our quest for q*. However, this does not imply that the fixed cost is irrelevant if we need to decide whether our business should be shut down for good! Indeed, we should also check whether overall profit
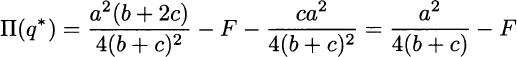
is positive. We see that we should produce only if
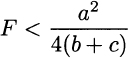
Leave a Reply