In Section 12.2.1 we dealt with a production planning problem within an assembly-to-order (ATO) framework. There, we disregarded demand uncertainty and built a deterministic LP model. Now, in order to make the model a bit more realistic, we represent demand uncertainty by a scenario tree and adopt a two-stage stochastic linear programming framework:
- First, we decide how many units of each component we should build, subject to manufacturing capacity constraints. This first-stage decision sets the total production cost.
- After receiving customer orders, we use available components to assemble finished goods. The assembly plan should maximize revenue; the cost term in the profit function is fixed by the previous decision (if we neglect assembly cost); if components are insufficient to meet customer orders, we lose profit opportunities; if too many components are available, they are scrapped, with a possibly considerable loss of money. We see that this problem is a generalization of the basic newsvendor model. The optimal use of available components is a second-stage decision, contingent on the realization of a specific demand scenario.
Of course, we cannot maximize profit, because it is a function of random variables (demand for end items), as well as our decisions; nevertheless, we may maximize its expected value.18 To be concrete, let us solve the same problem instance as in Example 12.10. Economic and technical data are given in Tables 12.1, 12.2, and 12.3. The only difference is in demand uncertainty. There, we assumed perfect knowledge of end-item demand. Now we assume the scenarios represented in Table 13.1. Let us denote the set of scenarios by S. For each scenario s ∈ S, we have demand 
, for all end items j ∈ J, and the probability πs. In the table, we consider only three scenarios, S1, S2, and S3. We also show the expected value of demand, under the assumption that the three scenarios are equally likely. Please note that expected demand is just the deterministic demand that we used in Table 12.3, when we solved the deterministic version of the model. Hence, the solution we obtained there is what we would get, if we ignored demand uncertainty by considering only expected demand. We recall that the deterministic solution was
Table 13.1 Demand scenarios and expected value of demand.
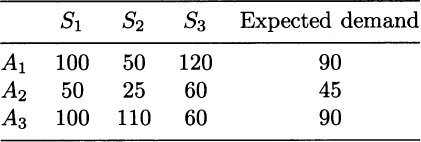
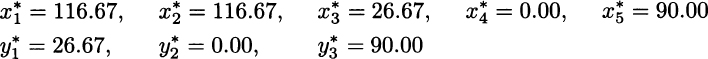
with “optimal profit” 3233.33. We should immediately understand that this is the value of the optimal profit in the deterministic model, but is not the true optimal profit, as this does not make any sense in decision-making under risk. To build a two-stage stochastic programming model, we need to introduce suitable decision variables at each stage of the decision process:
- The first-stage decision is the amount of components that we produce: xi, i ∈ I; this decision is the same as in the deterministic model, as here-and-now decisions are not scenario-contingent.
- The second-stage decision is the amount of end items that we assemble, contingent on the demand scenario:
, j ∈ J, s ∈ S. Note that, with respect to the deterministic model, we add a scenario superscript, since second-stage decisions are scenario-contingent.
Now we may extend the deterministic model as follows:
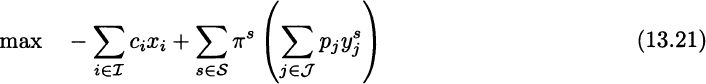
The big change in this model, with respect to the expected demand model [(12.22)–(12.24)], is that demand uncertainty is taken into account explicitly. In practice, we just implement the production plan (first-stage decisions xi) and develop a contingency plan for the assembly operations (second-stage decisions ). Only when demand is realized do we choose one among the contingency plans. With three scenarios, we have three contingency plans. Clearly, there is little hope to fully capture demand uncertainty with a handful of scenarios, and actual realized demand will probably differ from that assumed in any scenario. In practice, once demand is realized, we simply have to write a second model for assembly decisions, where we need to meet the realized demand with a limited availability of components, so as to maximize revenue. The aim of scenarios is to make here-and-now decisions not myopic and as robust as we can; second-stage decisions need not be immediately implemented.
Going into the details of the model above, the objective function (13.21) consists of a first-stage (deterministic) term, accounting for the cost of components, along with a second-stage term, which is the expected revenue from selling end items (not including component cost); the expected value is computed by summing the revenues for each scenario s, weighted by the scenario probabilities πs. The capacity constraint (13.22) is unchanged, because it pertains to the first-stage decisions only. The market demand constraint (13.23) is now scenario-dependent, as it considers the stochastic demand . Finally, constraint (13.24) links the two stages, stating that assembly is constrained by component availability, for each end item j and each scenario s. By solving this model with the numerical data of our toy example, we obtain the following solution:
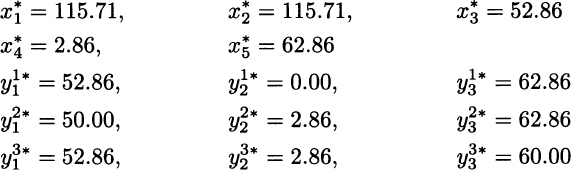
The expected profit for this solution is 2885.71. As we pointed out, the real outcome of the model is the set of the first-stage decision variables 
. Observing the component production plan, we immediately see a qualitative difference with respect to the model disregarding uncertainty: It is less extreme. We do not produce a large amount of component c5, because we do not place a risky bet on high sales of A3. In fact, scenario S3 would prove a disaster for the deterministic solution; in that scenario, sales are lower for A3, but we could not react because we do not have enough specific components for the other end items. So, 30 specific components c5 would be scrapped; furthermore common components would be scrapped as well, since they cannot be used to assemble other end items for the lack of the related specific components.19 The stochastic model, on the contrary, reduces production of c5 and increases production of specific component c3, which is needed to support assembly and sales of A1; even a small amount of component c4 is produced, in order to support the least profitable end item A2, which helps in using common components when sales are low for other end items. While there is a big difference in terms of specific components, we see that, as far as common components are concerned, the solutions of the deterministic and the stochastic solutions are essentially the same. There is a good reason for this, as common components are a flexible resource, which can be exploited to assemble different end items. Moreover, the demand for common components is the sum of the individual demands for the end items, and by aggregating demand we often reduce uncertainty. Indeed, this risk-pooling effect is what we try to exploit in assemble-to-order systems. However, it is also important to note that when end-item demands are strongly correlated, the risk-pooling effect is considerably reduced. In such a case, we should expect that even the produced quantities of common components differ in the deterministic and the stochastic models. Another relevant factor is capacity: If this is so tight that we may sell whatever we are able to produce, a simple deterministic model could be a viable option.
But how do the two solutions compare in terms of profit? The objective function from the solution of the second model is 2885.71; apparently, the stochastic solution is worse than the deterministic solution, whose optimal profit was 3233.33. But this comparison makes no sense, as doing so we are actually comparing two different situations, rather than two different solutions. This simply proves that we would rather face a certain demand rather than an uncertain one. The objective function of the first model is neither the true profit, which is uncertain, nor its expected value. It would be the optimal profit, if we knew that the average demand scenario will be realized for sure. In the first model [(12.22)–(12.24)] we pretend to know the end-item demand, and we get the illusion of higher profits. In order to compare the two solutions, we should fix the production plans for components that the two models propose, and then we should solve a set of second-stage problems, where we optimize assembly of end items subject to component availability, for different demand scenarios. More formally, given the vector x* of first-stage optimal decisions of whatever model, we should solve the following second-stage (recourse) problem for each scenario s in S:
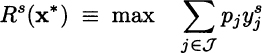
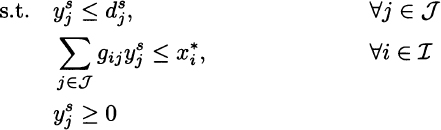
where Rs(x*) is the optimal revenue that we collect under scenario s, given the first-stage solution x*, when making optimal use of the available components to meet demand. Note that in this model the component availability is given, either by the stochastic or by the deterministic, expected-value model. Whatever the case, the resulting expected revenue is
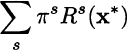
Expected profit for an arbitrary solution is obtained by subtracting its first-stage cost from this second-stage expected revenue.20 To evaluate the deterministic solution, we should plug it into this model. In the case of scenario S1, the optimal assembly and sales plan is
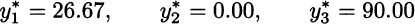
and the same holds for S2. The bad news is that if scenario S3 occurs, we are in trouble, because the high-risk solution does not fit demand very well. The optimal assembly and sales plan would be
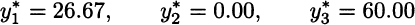
This is a pretty bad scenario with low sales and corresponding low profit. As we said, we must compute revenue for each scenario, multiply it by its probability, sum everything to get the expected value, and subtract the component cost from the first stage. The expected profit from the deterministic solution turns out to be 2333.33, and is much lower than what the objective function of the deterministic model [(12.22)–(12.24)] predicts (3233.33), based on one average-case scenario. The percentage improvement of the stochastic solution with respect to the deterministic one is, in terms of expected profit for the three scenarios,
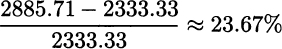
Clearly, we cannot extrapolate general results from a small toy example. Indeed, the advantage of using a stochastic model is striking here, because specific components have a large impact. In a case featuring much more component commonality, the result would be less impressive. Furthermore, we have assumed that unused components are scrapped, which need not be the case. They could have some salvage value, and we could have a multistage problem where remaining components can be used at later stages.
Leave a Reply