A MOTIVATING EXAMPLE: ECONOMIC ORDER QUANTITY

Before getting into formal details of calculus, it is essential to arm ourselves with some motivation for doing so. In management science, we often want to relate decisions to cost or profit. This is necessary in order to find an “optimal” decision yielding the best performance in some well-specified sense. We should quote “optimal,” because our decision is just optimal with respect to our cost or profit model. It is often said that all models are wrong but some are useful. Indeed, a model can be a quite rough representation of a possibly complicated and uncertain reality. Still, it can be useful to sharpen our understanding and to find a good decision. We should never forget that a quantitative model is just a decision aid and not a magical oracle. A case in point is the economic order quantity (EOQ) model. This is a somewhat old-style, archetypal model for inventory management, relying on a lot of debatable assumptions; yet, it can have some value in practice and is a good way to show mathematical modeling and calculus in action.

Imagine that you are in charge of managing the inventory of an item at a retail shop. Inventory is depleted at a rate depending on demand, and every now and then you have to replenish inventory by issuing a purchase order to a supplier, or maybe a production order to your own manufacturing facility. To keep it simple, let us assume that demand is perfectly constant in time and let d denote the demand rate. The demand rate is the demand per unit time, such as 10 items per day or 75 items per week. The specific time unit is not important, provided we are consistent in specifying all of the relevant data.

Which kind of decisions are you supposed to make? Actually, there are two decisions involved here:

1. When to order
2. How much to order

The first decision, in an ideal world, is actually trivial. By “ideal” world we mean a world in which there is no uncertainty involved:

• Demand is perfectly predictable (even constant, under our assumption); we also assume that demand is “fluid,” in the sense that we approximate the discrete flow of items out of inventory, one piece at a time, as a continuous flow.
• The time it takes to get a shipment from the supplier is fixed and known; this time is known as lead time or time to delivery.

In this setting, you should issue a replenishment order when inventory reaches a level corresponding to demand during lead time. For instance, if time to delivery is 2 days and the demand rate is 10 items per day, it is easy to see that you should issue an order when your inventory level decreases to 20 items.² Doing so, you will receive the new stuff exactly when you run out of stock! Clearly, such magic does not happen in real life, but for our little example we may ignore issues related to variability in time to delivery and timing of orders.

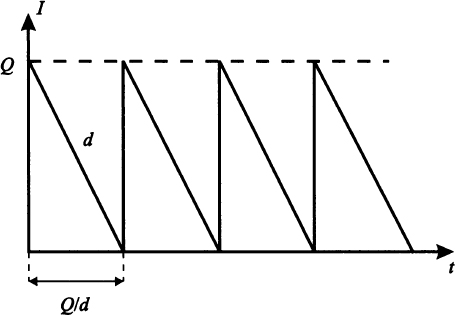
Fig. 2.1 Time evolution of inventory levels in EOQ model.

As to the second decision, since demand is constant, it is reasonable to assume that whenever you replenish, you always order the same amount, i.e., your preferred order size. Let Q be the order size we choose and, without loss of generality, assume that we start with Q units on hand. The resulting inventory pattern will look like Fig. 2.1, where I denotes the inventory level and t denotes time. We see that the inventory pattern is periodic, as we issue an order every Q/d time units. For instance, if the demand rate were 100 items per week, an order size Q = 300 would result in a replenishment order every 3 weeks. In practice, the inventory plot would be a stepwise function, as we sell one item at a time, and not fractions of items; yet, if demand volume is large enough, a continuous pattern like the one in the figure is a fair approximation. The case of sporadic demand for a niche product should be addressed by a different modeling approach.

So, under our quite strong assumptions, we have just one decision to make: Finding the right amount Q to order, i.e., the economic order quantity (EOQ). Indeed, this is a matter of compromise between conflicting needs:

• Imagine that, whenever you issue an order, a fixed charge³ is incurred. For instance, if your supplier ships a container, quite reasonably the shipping charge will include a fixed component that does not depend on what and how much is transported. Hence, from this perspective you would like to order a rather large amount, whenever you replenish, in order to spread the fixed ordering charge on as many items as possible. Put another way, the less orders are issued per year, the better.
• On the other hand, you would like to order just a few items quite often. Doing so is important when items, such as fresh produce, are perishable and their limited shelf life precludes stocking large amounts. Perishability should not be confused with a similar issue, obsolescence, which is typical of fashion products or items characterized by a fast pace of technological innovation, such as consumer electronics.⁴ Even if you do not consider such issues, there is a good financial reason to keep inventories low. When you receive a shipment from your supplier, you pay her, and this means that you have tied up some liquid cash to your inventory. When you sell, you will get your money back, plus a profit margin, but having too much liquidity immobilized there may be a bad idea. Apart from this opportunity cost of capital, large on-hand inventories also imply high insurance costs. Even worse, you may end up with a huge inventory of a slow-moving item, locking liquidity and precluding the purchase of items that are in demand, unless you borrow money from a bank, incurring possibly high interest rates.

Note that, in our setting, we should not consider profit, since we are assuming that we will satisfy all of the customers anyway; hence, our problem is just satisfying demand at minimum cost, and this in turn requires spotting the right compromise between the two conflicting requirements above. How can we do that?

There are three tasks that we should accomplish in sequence:

1. We should make the relationship between the decision Q and the total cost explicit. To this aim, we may write down a function C_tot(Q) mapping order size Q into total cost; to be more precise, we will consider the average total cost per unit time. To fix ideas, we assume that our time unit is exactly one year.
2. We should sketch a graph of the total cost function to see what impact our decisions have on average total cost per year.
3. Finally, we should find the best decision, i.e., the optimal order size Q*, such that the cost function attains its minimum.